1 引 言
地铁、地下快速路等地下交通项目因其显著的交通拥堵缓解作用,在多山的城市地区尤为重要。这种建设项目常涉及大量的隧道工程,其中钻爆法作为一种常见的隧道施工方法,在实施过程中会产生爆破振动,扰动在建隧道和周边构筑物,影响隧道本身和周边建筑物的结构安全。因此,对隧道爆破振动进行有效的监测和分析,是确保建设安全和降低环境影响的关键。
爆破振速能较好地反映爆破振动强度,是评价爆破安全的判据之一。诸多学者对隧道爆破施工过程中地表质点振动速度进行研究,如王松青等、李小刚等、肖文芳等对隧道爆破振动进行监测,发现峰值振速随爆心距的增大表现出先增大后减小的规律。朱根桥等通过对隧道爆破振动进行监测发现,邻近隧道和建筑物的振速均远低于规范限值,说明既有隧道形成的临空面对于吸收和释放爆破振动能量的作用较大。朱正国等研究了常规爆破方式下立体交叉隧道动力响应规律,确定了安全振速标准及不同影响程度的安全范围。李术才等采用MIDAS-GTS有限元分析软件进行三维数值分析,揭示了爆破施工对既有隧道变形及内力的影响规律,同时给出了合理的爆破振速控制指标。
隧道爆破开挖过程中会对土层产生扰动,引起土体变形,使邻近隧道以及地表建筑物产生不均匀沉降、倾斜和开裂等。杨钊等通过数值仿真计算和现场监测,探究了施工爆破对地表建筑的影响规律。宋战平等结合建(构)筑物爆破振动安全判据对模拟监测点的振动影响进行评价并对振动控制参数进行优化,从而降低隧道爆破对邻近结构的振动影响,提高了隧道爆破质量。于建新等基于现场监测试验,对双线大跨公路隧道后行洞开挖爆破时邻近先行洞的振动响应特性进行了研究。王建秀等则运用有限元分析方法,对下穿段地表沉降规律和控制方法进行探讨。何忠明等针对地表受隧道开挖及爆破影响发生的沉降问题,采用FLAC3D软件模拟分析了隧道爆破开挖引起的地表沉降及其规律。
上述研究大多集中于隧道爆破施工过程中的质点振动速度、地表位移沉降以及地表建筑物的响应规律研究,且以数值模拟研究为主,较少涉及隧道爆破振动影响下的地表沉降规律相关性分析研究。因此,本文以珠海兴业快线(北段)东线隧道爆破开挖为依托,对爆破施工产生的振动速度和频率进行实时监测并对监测数据进行分析;同时,基于Copula理论分析在隧道爆破开挖荷载作用下地表沉降规律,以便为工程实践提供参考。
2 工程概况
珠海兴业快线(北段)工程为珠海市最大的市政交通项目,是珠海市衔接“粤港澳大湾区”的重要组成部分,总投资约64亿元。兴业快线(北段)全长约17.1 km,承担中心城区内部南北向快速通道,向北至中山、深中通道方向,向南向延伸至人工岛(港珠澳大桥),将为珠海东部城市发展轴的快速交通提供服务。线路呈“Y”字形,南北走向,东线起于唐乐路,沿线下穿中大、鸡山村,西线起于哈工大路,沿线上跨金唐东路,东西线以隧道穿越凤凰山,以桥梁形式合并后继续以隧道穿过凤凰山,沿兴业路下穿梅华路,其中矿山法段长12.3km,矩形暗埋段长3.0km,桥梁段长1.8km。该工程需要打通加林山、板障山、凤凰山3座大山,需要进行大量的爆破工程。隧道穿越的地区地质复杂,分布有不同的岩层,地形条件多变,山谷沟壑交错,采用钻爆法进行隧道施工对环境影响较大。该工程合并段隧道小里程端位于大镜山水库附近,周边建筑物密集,东线隧道大里程端位于鸡山村,周边有部队、学校、民房,建筑物密集。如何快速施工同时确保周边建筑物安全、减少对周边居民的影响是工程的重难点,其中爆破振动的监测研究尤为重要。
3 爆破振动现场监测
3.1 监测目的与控制标准
隧道爆破施工对建筑物的影响主要是爆破振动的影响。目前爆破振动对建筑物安全的影响主要是依据安全振动速度来判断,在珠海兴业快线(北段)项目隧道的爆破施工中,附近的房屋受损严重,出现大量裂缝,如图1所示。

图1 建筑物开裂
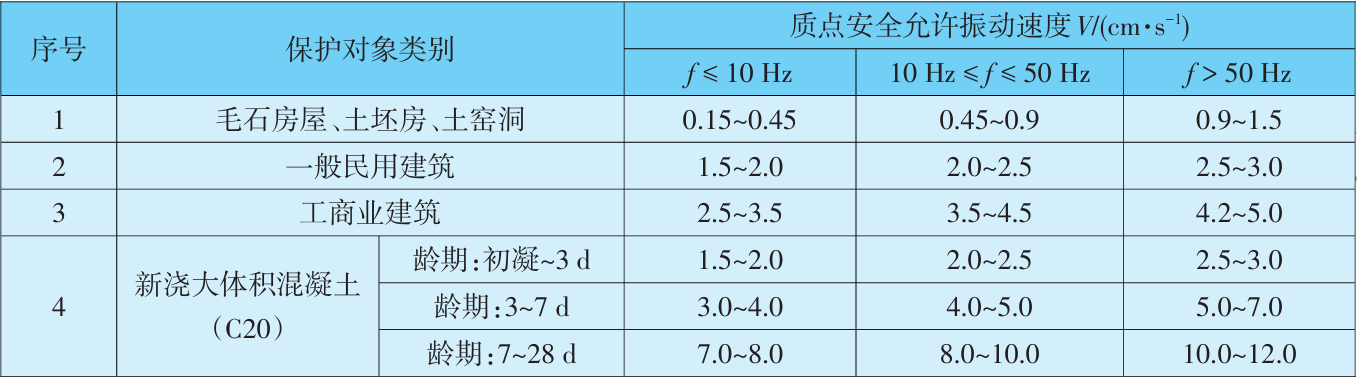
建筑物结构对爆破振动的动力响应受多种因素影响,目前尚无具体的计算公式。为全面评估地表建筑物在爆破振动作用下的安全性,需根据爆破地震波和建筑结构特性进行现场振动测试。爆破振动监测的目的在于通过现场监测与信息反馈,研究隧道爆破荷载作用下内部结构振动速度分布特征,准确预测质点振动速度,以确保爆破工程的安全运行并减少对地面建筑的不利影响,及时发现潜在问题,确保施工安全。对爆破振动进行现场监测,目前所用的爆破安全控制标准见表1。
表1 爆破振动安全允许标准
3.2 振动速度与频率监测
在东线隧道出口周边采用TC-4800爆破测振仪对建筑物地表进行爆破振动监测,对爆破在建筑物中引起的隧道径向(X)、切向(Y)和垂向(Z)的振速和频率进行监测,为保证监测数据的准确性,根据爆破振动传播特性、测振仪器技术指标等相关测试结果,在隧道出口周围共布置8个监测点,如图2所示,按距离隧道的远近划分为近爆源区(100m范围)和远爆源区(200m范围),具体监测点信息见表2。
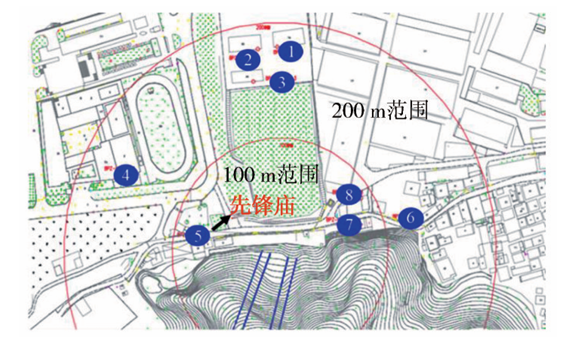
图2 爆破振动监测点示意
表2 爆破振动监测点信息

3.3 隧道出口断面沉降监测
爆破过程中产生的地震波在土体中的传播可能会改变周围土体结构,引起隧道周围地基的不均匀沉降,从而导致结构出现破坏。因此,对于隧道周边的土体沉降监测也至关重要。为分析爆破振动对隧道沉降的影响,在隧道出口左线、右线分别布置沉降监测点,如图3所示。隧道左线、右线均布设了2排监测点。其中,左线第1排共布设20个监测点,编号为z1-1~z1-20,第2排共设置8个测点,编号为z2-1~z2-8;右线第1排共布设25个测点,编号为y1-1~y1-25,第2排共布设8个测点,编号为y2-1~y2-8。
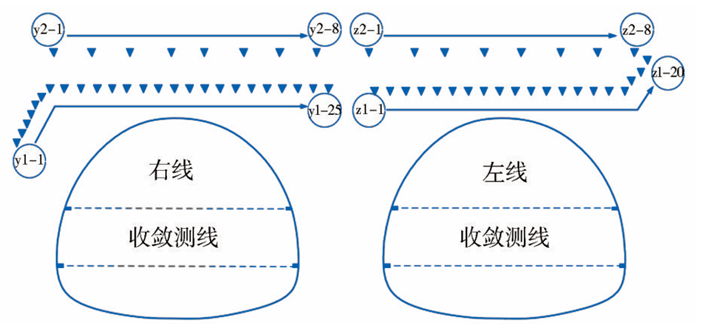
图3 沉降监测点布设示意
4 爆破振动响应分析
4.1 振动速度与频率分析
提取隧道周边8个监测点3个月的监测数据,得到X、Y、Z方向的振动速度如图4所示,统计得到X、Y、Z方向上振动速度最大的前3个监测点数据见表3。由图4和表3可知,在3个方向地表质点振速随爆心距的增大而减小,近爆源区(100 m范围内)监测点BPZ-5、BPZ-7和BPZ-8的振动速度较大,各测点在Z方向的振速大于X、Y方向振速,且监测点BPZ-7的振速在3个方向均最大,其在Z方向的最大振速为0.73cm/s,仍满足爆破振动安全允许标准。随着水平距离的增加,在距爆源更远区域(200 m范围内)X、Y、Z3个方向间的振动速度差别较小,各测点在Z方向的振速略大于X、Y方向振速。
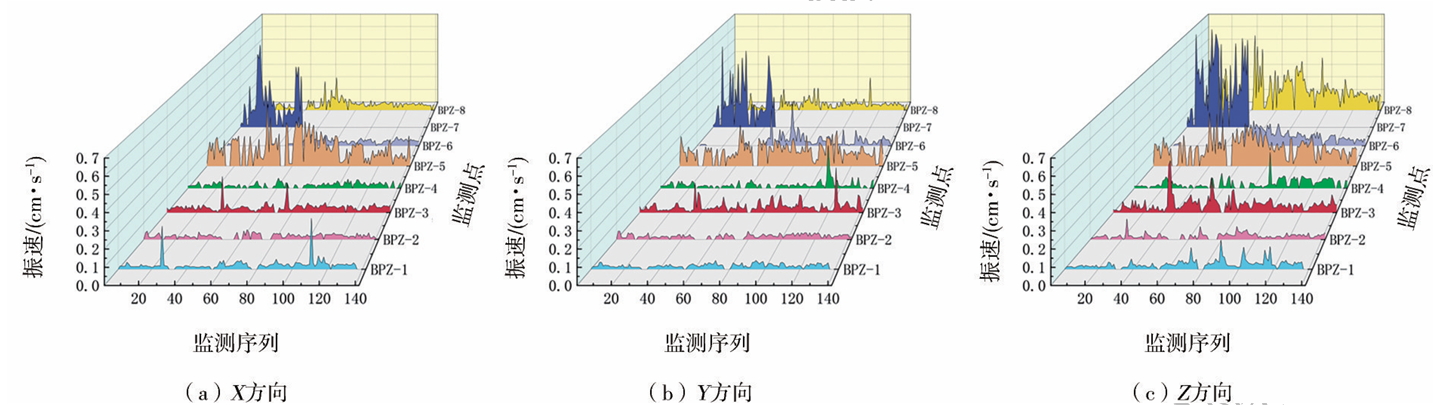
图4 监测点BPZ-1~8在X、Y、Z方向的振动速度
表3 监测点BPZ-5、BPZ-7和BPZ-8的最大振动速度

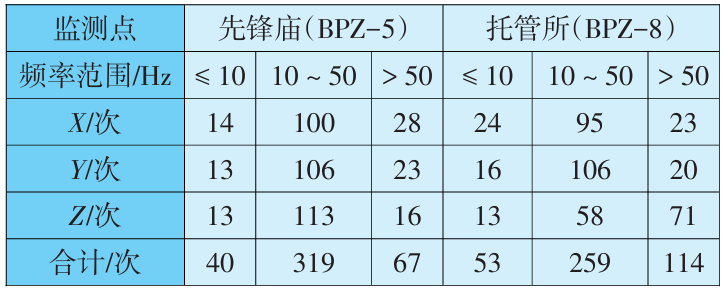
由表1可知,安全允许振动速度范围与振动频率相关,在不同的振动频率下,安全允许振速范围也有所不同。当质点的振动频率相对较低时,所对应的安全允许振动速度较小;若质点处振动频率较高,则该处的安全允许振动速度就相对较大。各测点在X、Y、Z 3个方向的频率变化如图5所示,可知相较于振动速度而言,在地表距离爆心不同水平距离范围内,各测点在不同方向的振动频率变化差异较小。监测点BPZ-5和BPZ-8的爆破振动频率分布次数统计见表4,可知在统计的142次监测数据中,地面质点振动频率大部分集中在10~50Hz的范围内,但X方向振动频率有14次低于10Hz,Y方向和Z方向振动频率则有13次低于10Hz。按照表1中爆破振动安全允许标准的规定,该频率范围对应的爆破振速安全标准范围为1.5~2.0cm/s。因此,为了保留一定的安全储备,该工程爆破安全振动速度安全标准设定为1.5cm/s。
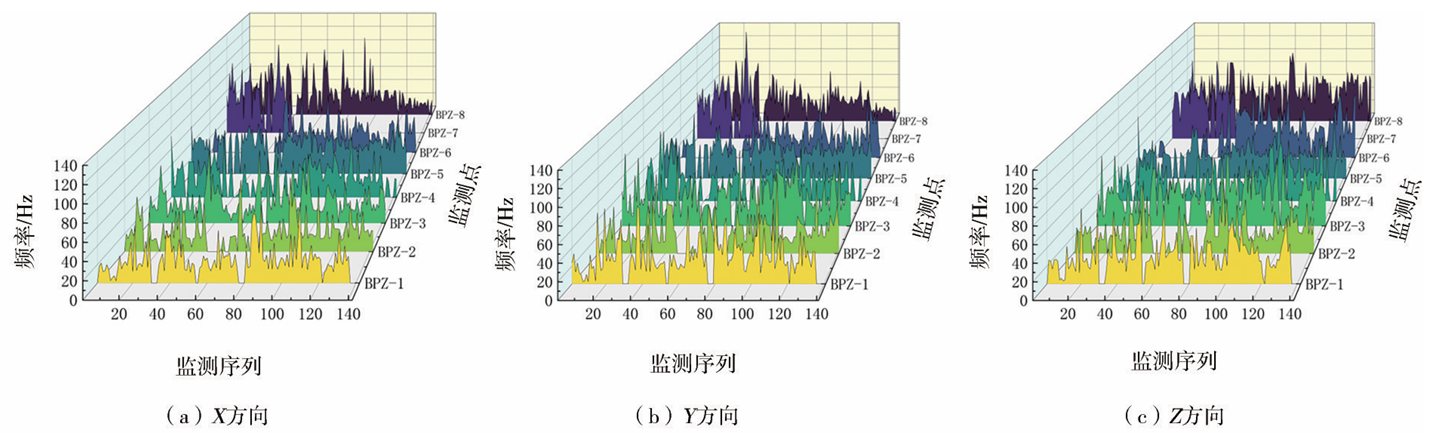
图5 监测点BPZ-1~8在X、Y、Z方向的振动频率
表4 监测点BPZ-5和BPZ-8的爆破振动频率分布次数统计
4.2 隧道沉降分析
获取与爆破振动相同监测时间段内3个月的隧道出口沉降速率数据,得到沉降速率变化曲线如图6所示。图6中,正值表示地表隆起,负值表示地表沉降。由图6(a)可知,隧道左线第1排监测点以沉降为主,且沉降速率不断增大,不同监测点间沉降速率相差较大,靠近隧道右线的监测点z1-4沉降速率最大,最大沉降速率为11.4mm/d。由图6(b)可知,隧道左线第2排监测点(除监测点z2-2以外),均表现为隆起,且沉降速率变化趋势较为接近。由图6(c)、(d)可知,测点y1-25表现为沉降,且沉降速率不断增大,最大沉降速率为7.6mm/d;其余监测点变化趋势较为相似,均表现为先隆起后沉降。
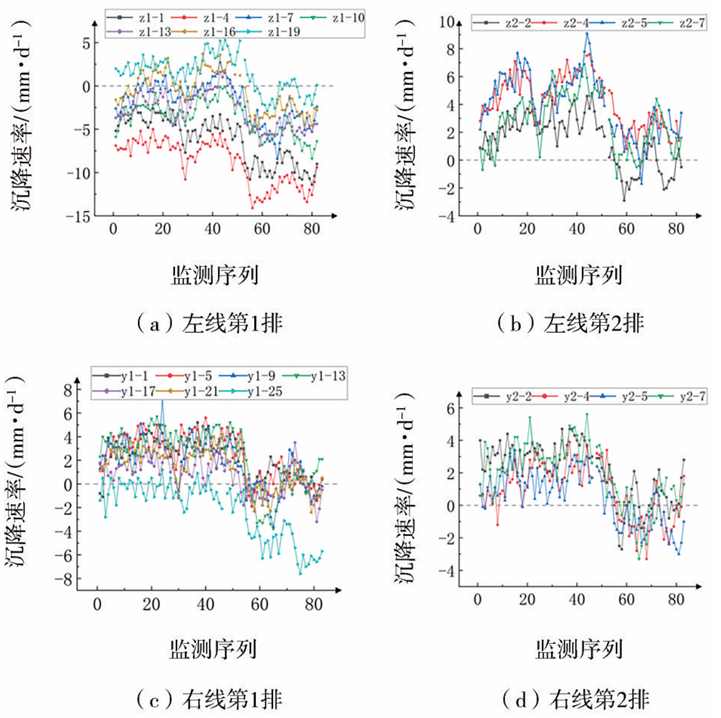
图6 隧道左右线各监测点沉降速率曲线
隧道左右线各测点累计沉降量如图7所示,可知隧道的最大累计隆起量、沉降量均出现在隧道左线。其中,监测点z1-4最大累计沉降量最大,为9.4mm,监测点z2-5隆起量最大,为3.4mm。位于隧道左、右线间的监测点变化量较大,应重点关注该区域内的沉降变化。
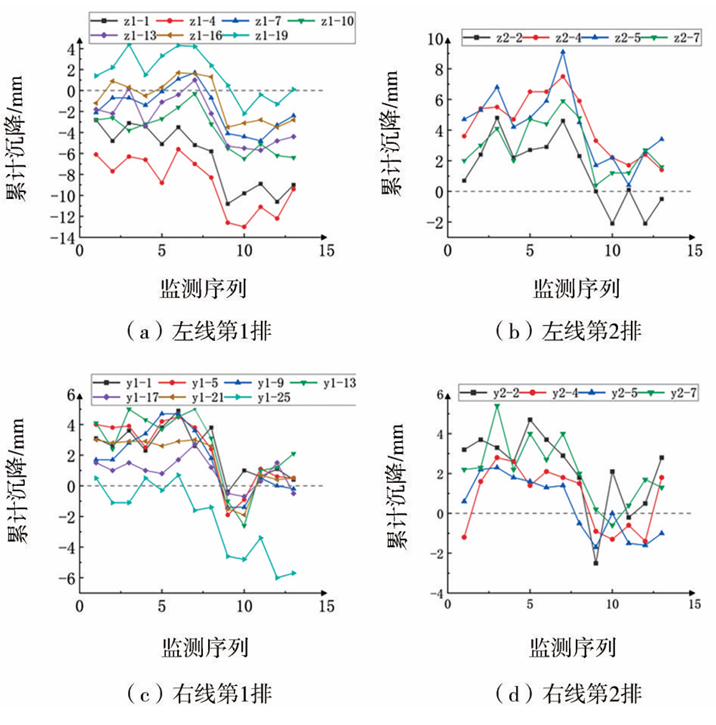
图7 隧道出口累计沉降
5 隧道结构可靠性分析
基于4.2节监测成果,选取左线、右线隧道沉降速率最大的监测点z1-4和y1-25,以及左线隧道沉降速率最大的监测点z1-4和隆起速率最大的监测的z2-5,分别进行爆破振动影响下的隧道沉降相关性分析,从而建立隧道结构可靠度分析模型。
5.1 Copula理论与模型评估
Copula函数定义为[0,1]2空间中边缘分布为[0,1]区间内均匀分布的二维联合分布函数:
F(x1,x2) = C(F1(x1),F2(x2); θ) = C( μ1,μ2; θ) (1)
式中:F(x1,x2)为变量X1、X2的联合分布函数;F1(x1)和F2(x2)分别为变量X1、X2的边缘分布函数;C为Copula函数;θ为Copula函数的相关参数。
在确定Copula函数的相关参数θ之后,可得到Copula联合分布函数和Copula联合概率密度分布函数,从而通过AIC(Akaike Information Criterion) 准则和BIC(Bayesian Information Criterion)准则,选取最优Copula函数,AIC、BIC值最小的函数类型即为最优函数。计算公式为:
AIC = 2k- 2ln(L) (2)
BIC = ln(n)k- 2ln(L) (3)
式中:L为似然函数;n为样本大小;k为参数数量。
由4.2节可知,隧道左线第1排监测点中z1-4的沉降速率最大,左线第2排监测点中z2-5的隆起速率最大;隧道右线第1排监测点中y1-25的沉降速率最大。因此,为分析左、右线隧道的沉降相关性以及同线隧道中沉降与隆起的相关性,本文采用Copula函数建立监测点z1-4与z2-5、z1-4与y1-25的相依性模型。
研究中使用较多的Copula函数主要有阿基米德Copula函数簇(如Frank、Clayton、Gumbel、Joe)和椭圆Copula函数簇(如Student-t、Gaussian),为了方便计算,以往研究一般直接采用GaussianCopula函数建立相依性模型进行分析。然而,实际变量间并非总是服从Gaussian相关结构,故本文采用上述6种Copula函数以及BB1(将Gumbel和Clayton结合)和BB7(Gumbel和Frank结合),用于建立变量间的离散相依性模型并选出最优Copula函数。
监测点z1-4与z2-5、z1-4与y1-25的散点图如图8所示,2个监测点间均具有一定的正相关性,因此,在构建模型时,要注意考虑参数间的相依性。
最优Copula函数的识别,首先需要对选取的Copula函数进行参数估计,根据参数间Kendall相关系数,得到Copula函数的相关参数,进而通过式(2)和式(3)得到不同Copula函数下的AIC与BIC值,见表5。根据表5绘制不同Copula函数下的AIC与BIC值对比图如图9所示。由图9可知,采用FrankCopula表征监测点z1-4与z2-5、监测点z1-4与y1-25之间相关结构时得到的AIC与BIC值最小。
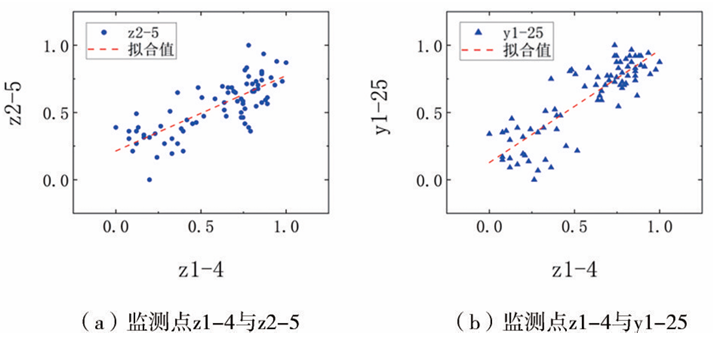
图8 不同监测点沉降分布散点图
表5 不同Copula函数计算的AIC与BIC值

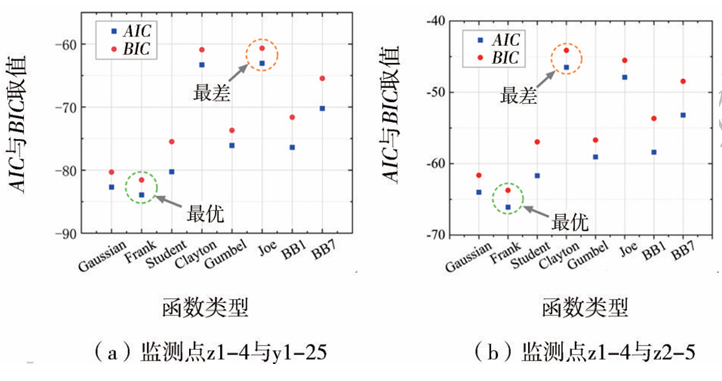
图9 不同Copula函数下的AIC与BIC值对比
为更全面且直观比较不同Copula函数之间的差异,对不同Copula函数进行随机变量模拟,如图10所示。图10(a)为不考虑参数的相依性,即参数独立情况下的散点图,该情况并不能较好地反映原始数据的分布趋势;图10(b)~(e)为模拟次数N=5000时利用Copula函数模拟计算生成的各监测点数据,其中红色三角形表示原始的实测数据,蓝色圆点表示模拟生成数据。其中,Gumbel、Joe以及BB7Copula主要处理上尾依赖,即在极端情况下变量间的依赖性;Clayton Copula主要处理下尾依赖;BB1和Student-tCopula既可处理上尾依赖也可以处理下尾依赖。
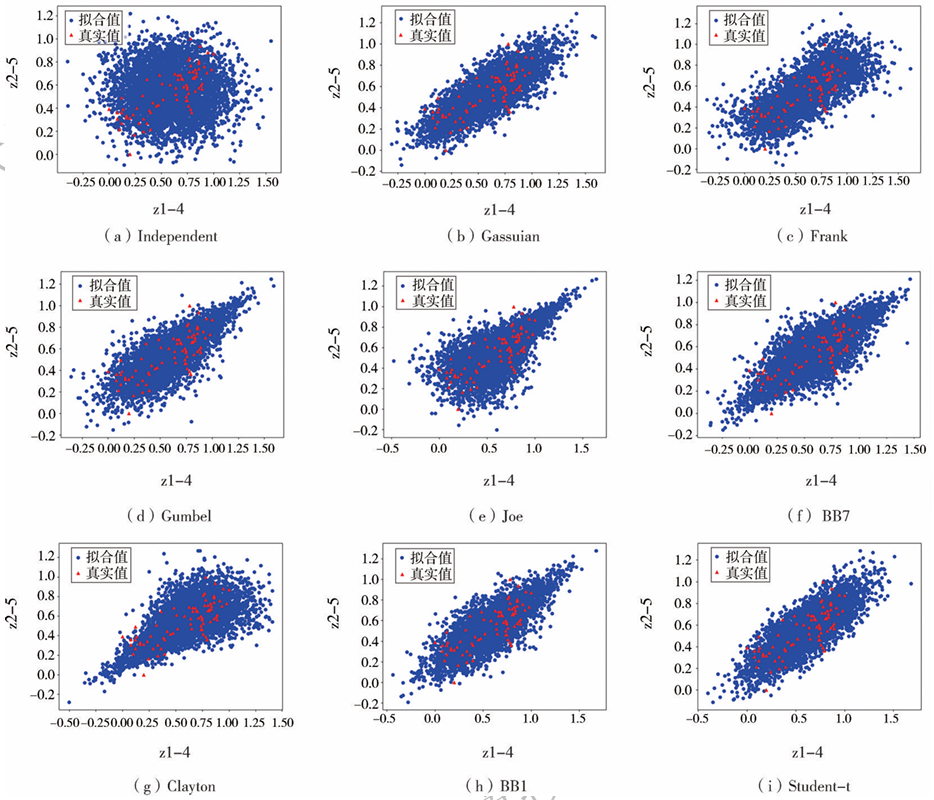
图10 监测点z1-4与z2-5不同Copula模型模拟散点图
由图10可以看出,基于Copula函数构建的相依性模型进行模拟生成的散点相较于参数独立时更加集中,不同的Copula函数模拟结果对应分布具有不同的聚集特征。本文所研究的测点间并未存在较强的尾部依赖,采用FrankCopula模拟得到的散点聚集性较好,且计算得到的AIC与BIC值也最小。因此,描述测点间相关性的最优Copula函数为FrankCopula。
5.2 隧道结构可靠性分析
在隧道结构的可靠性分析中,通常将其视为一个串联系统,其特点是任何一个单独的失效模式都可能引起整个系统的故障。因此,本文考虑隧道结构的整体失效概率作为评估其可靠性的主要指标,即当2个监测点中有1个监测点的监测值未满足安全预警值,即判定为系统失效。采用蒙特卡罗模拟法确定系统的失效概率,其计算公式为:
pf= P(h1(X ) ≤0∪h2(X ) ≤ 0) (4)
hi( X )=kp- yi(X) (5)
式中:pf为失效概率,即满足要求范围之外的散点数与散点总数之比;hi(X)为功能函数;X为沉降值;kp为满足规范要求的沉降速率监测预警值;yi(X)为结构样本值。
由于结构失效概率一般很小,为更直观了解,可采用可靠度指标度量结构构件的可靠程度。可靠性指数β为:
β = Φ-1(1- pf) (6)
式中,Φ-1(∙)为标准正态分布函数Φ(∙)的反函数。
通过蒙特卡罗法模拟得到5000组数据点,根据式(4)计算出隧道结构失效概率pf。根据工程要求,本文沉降监测速率预警值为5mm/d,由式(6)计算得出其可靠性指数β,结果见表6。
表6 失效概率pf与可靠性指数β

由表6可知,采用不同Copula函数所计算出的pf和β值不同,监测点z1-4与z2-5采用ClaytonCopula计算的β=-2.02,与其他Copula函数明显不同,这意味着该Copula不适合构建Copula模型。由于Frank Copula是最适合的Copula,因此需要密切注意Frank Copula计算的pf和β值。根据表6,可知FrankCopula 计算的β值为-2.64,这是由于监测点z1-4的沉降均处于预警值(5mm/d)之下,故所计算的失效概率较高,从而导致可靠度指标β为负值,即结构的失效风险高于可接受水平。
针对上述情况,实际工程中采用数值模拟手段对隧道开挖步长、各导洞掌子面间距、仰拱间距、锁脚锚杆、对拉锚杆等施工参数进行分析。同时,将隧道开挖时的围岩内部位移情况、围岩压力分布、地表沉降大小、不同开挖段拱顶沉降情况以及不同位置锚杆应力分布等现场监控量测数据与模拟数据进行对比,以此优化数值模型设置和边界条件设置,为后续隧道的开挖与支护工作提供指导。即根据围岩等级选取不同隧道开挖方式,当围岩等级为Ⅰ、Ⅳ、Ⅴ级时分别采用台阶法、CD法和导坑法进行施工,从而尽可能减小因沉降而导致隧道结构失效的风险。
此外,还需注意保护监测点以避免被破坏,并加强对隧道及其周边仰坡的巡查和监测工作,以便及时反馈监测信息。同时,加强隧道结构的支护措施,实施短进尺和早期支护策略,特别是对锁脚锚杆等各类锚杆的施工,必须严格按照设计方案和相关规范执行。
6 结 论
本文通过现场监测数据,对爆破开挖引起的振动传播规律进行了研究,基于Copula理论分析沉降规律并进行隧道结构可靠性评价,主要结论如下:
(1)在爆源近区(100m范围内),随着爆心距的增大,各测点在垂向(Z)的振速大于X、Y方向振速;爆源远区域(200m范围内)X、Y、Z3个方向间的振速差别较小,各测点在Z方向的振速略大于X、Y方向振速。在地表距离爆心不同水平距离范围内,各测点在不同方向的振动频率变化不大,为了保留一定的安全储备,该工程爆破安全振速限值设定为1.5 cm/s。
(2)隧道的最大隆起和沉降均出现在隧道左线,最大累计沉降量为9.4mm,最大隆起量为3.4mm,均满足安全标准。位于隧道左、右线之间的监测点沉降变化量较大,实际工程中需注意对该区间监测点的保护,避免测点破坏;加强对隧道及周边仰坡的巡查和监测工作,及时反馈监测信息。
(3)选取隧道左、右线沉降变化最大的监测点构建相依性模型,设置沉降速率性能阈值进行隧道结构可靠性分析。不同Copula函数所得到的pf和β值不同,Frank Copula为最优Copula,Clayton Copula不适合构建Copula模型。在实际工程中,根据数据特征选取最优Copula函数用于精确表征参数的相依关系是很有必要的。
摘自《现代隧道技术》