深基坑开挖影响下深厚软土路基变形规律研究

0　引言

城市片区开发向地下空间发展,与此同时道路、建筑物等出现了许多由临近基坑施工带来的环境影响,如路面的不均匀沉降。当所引起的变形超过一定容许界限,将带来更严重的问题,比如地表开裂、管线断裂等。因软土具有含水量高、压缩性高、结构性强、强度低和流变性明显的特点,软土地区深基坑施工的环境效应更加明显。软土地区深基坑开挖的环境影响受到了持续的关注,为满足周围环境变形承受能力,软土地区基坑的设计理念逐渐由支护结构安全向变形控制发展。

国内外一些学者采用了数值分析、现场实测和经验公式等方法进行了基坑开挖变形的影响因素研究。朱志祥等采用数值研究表明,被动区加固能有效减小软土基坑围护结构侧向位移和地表沉降;康志军等针对上海软土地区的基坑,研究了被动区不同加固形式对基坑变形的影响,数值计算结果表明,合理的坑底加固措施能使基坑变形满足控制标准。李卓峰等以宁波软土某地铁基坑为例,通过实测和数值分析验证了坑底被动区加固能显著减小水平位移和地表沉降;郑俊杰等通过数值计算评估认为被动加固区参数变异性对软土深基坑变形行为影响有限;徐中华等以上海软土地区的排桩支护基坑80组实测数据为基础,统计认为支护桩最大侧向位移介于(0.1%~1. 0%)H之间;Xiang等通过研究软黏土中开挖深度、土体特性和支护结构刚度对支护墙变形的影响,建立了多元自适应回归模型来预测支护墙变形。

现有研究认为开挖卸荷所引起的环境效应受土体特性、坑底被动区加固、围护结构设置、开挖深度和开挖时序等影响。大范围深厚软土分布区域必须注意到先修路后进行地块开发,由于地下空间开发所形成的基坑近邻道路路面会产生不均匀沉降、开裂、管线破裂等问题,造成了大量返修与不良社会影响。路基工作性能与变形关系密切,同时路侧未处理软土对其变形也有一定的影响,其环境影响需要综合考虑。

本文以横琴深度合作区近邻某软土路基的深基坑工程为依托,根据先进行路基处理,后开挖基坑的实际工况,通过确定真空联合堆载预压处理后路基软土物理力学参数,建立考虑路基侧软土的数值模型开展基坑开挖卸荷对路基变形影响的研究,并将数值计算与实测结果进行对比分析,以掌握排桩支护条件下深厚软土路基侧向卸荷变形的影响因素和规律,为采取工程技术措施控制变形和减小基坑施工风险提供科学依据。

1　工程概况

依托项目位于横琴深度合作区,场地地层岩性自上而下可分为第四系人工填土层、第四系海陆交互相沉积层、第四系冲洪积层、第四系残积层及燕山三期基层。淤泥整个场地均有揭露,厚度为3.00~32.50 m,平均厚度为18.75 m,含水率高(46.1%~69.2%),区域软土深厚。场地地下水主要为上层滞水、潜水,水位埋深为约0.83 m。

软土路基处治技术主要为真空联合堆载预压:采用C型塑料排水板,正方形布置,间距1.0 m,打设深度按软土层底标高控制,最大不超过25 m,处理宽度控制在道路红线以外10 m,具体设计如图1,处理后固结度≥90%。

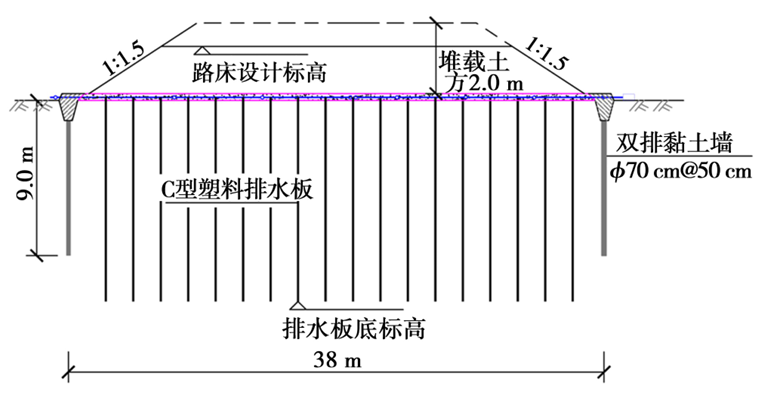
图1　真空联合堆载预压处理横断面设计

与此临近的勤政公寓项目基坑(图2),东侧和北侧临近风吹罗带路,拟建两层地下室,基坑面积1万多平,临近路基基坑深度约8.38 m。坑顶局部放坡喷混护面,采用间距为1 400 mm,直径为1 200 mm的排桩+一道混凝土撑的支护方案,支护桩外侧布设直径为800 mm的搅拌桩止水帷幕并深入黏土层,同时,坑底采用格栅式水泥搅拌桩对被动区进行加固。风吹罗带路软土路基和勤政公寓基坑的空间关系构成了典型的深厚软土路基侧的基坑开挖卸荷。

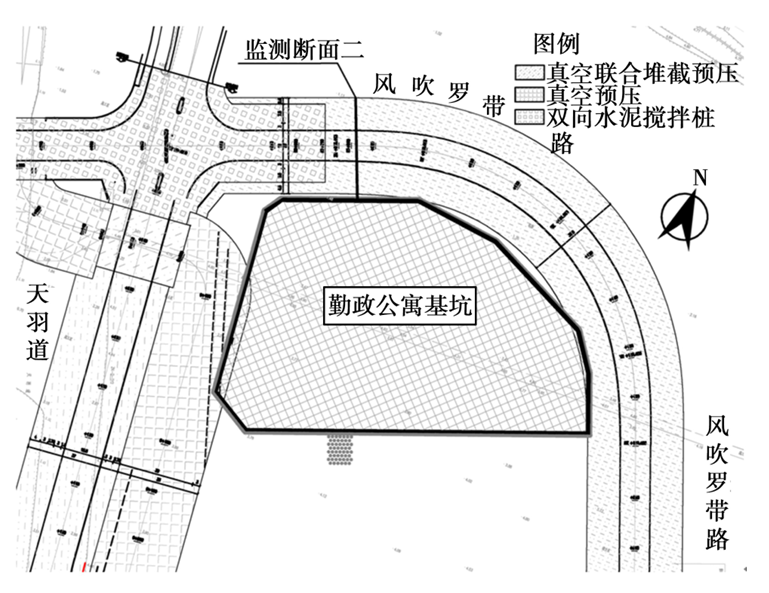
图2　工程平面位置关系

2　路基软土HS模型参数的确定与验证

硬化类的弹塑性HS模型(Hardening  Soil model)能考虑软黏土应变硬化特征、能区分加荷和卸荷且其刚度依赖于应力水平和应力路径,能很好地反映土体的非线性行为和塑性性质。

在软土路基填土层底以下5 m、10 m和15 m位置的淤泥(质)层中分别取样进行物性和力学性能测试,其结果表明处理后软土性质在空间分布上趋于一致,下面以软土路基填土层底以下5 m处试样为例对HS模型参数确定过程进行说明。

利用标准三轴固结排水剪切试验的应力路径,求得真空堆载联合处理后的淤泥(质)土层强度参数有效内摩擦角φ′=28. 1°和有效黏聚力c′= 10.8kPa。

HS模型以双曲线形式描述三轴应力应变关系:

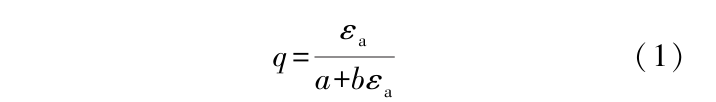
式中:a和b为具有物理意义的常数。

在P^ref=100 kPa时(即σ3 =100 kPa),标准三轴试应力应变实验数据如图3所示,采用非线性拟合的方式得到常数a=0.000 24和b=0.004 31,拟合结果见图3。显然当εa →∞,极限偏应力qa = 232 kPa。取实测偏应力的最大值185 kPa作为破坏强度qf ,可求得破坏比Rf =qf /qa =0.80。

E^ref ₅₀定义为参考围压下的主加载模量(kPa),即标准排水三轴试验q ε曲线中50%破坏强度(qf /2=92.5 kPa)对应的割线模量,利用式(1)进行反算,求得E^ref ₅₀ =2 505.5 kPa。

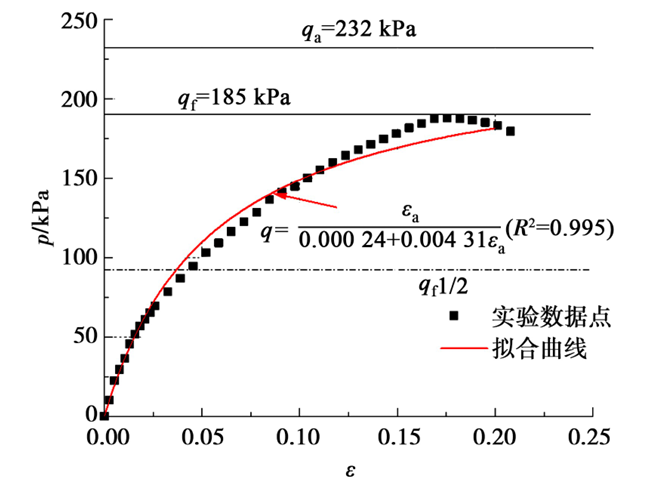
图3　标准三轴剪切试验应力应变关系

在标准固结试验中,假定竖向应变ε和竖向应力p存在如下双曲线关系:

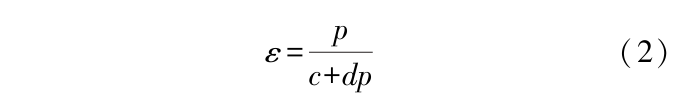
式中:c和d为常数。

E^refoed定义为固结试验中竖向压力p=100 kPa时对应的切线模量,式(2)对p求导可得:

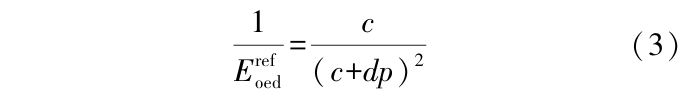
整理固结试验数据,绘制p ε关系曲线,如图4,利用非线性拟合得到式(2)中c=1012.422,d= 2.666。对应于竖向压力p=100 kPa时,根据式(3)求得Eref oed =1 615.8 kPa。

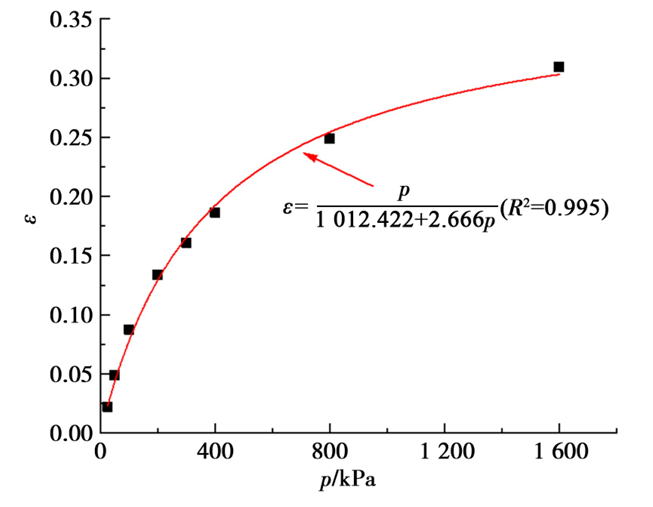
图4　标准固结试验中p ε曲线关系

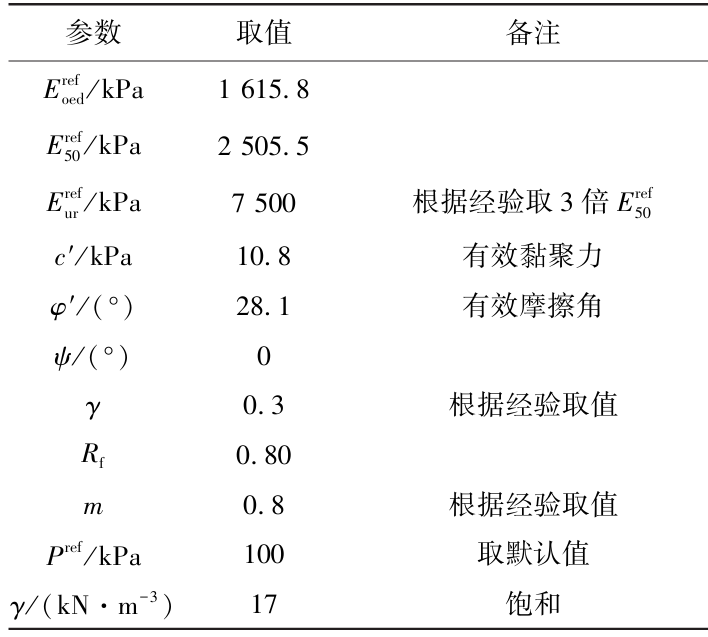
综合以上分析和物性试验得到HS模型相关参数,总结如表1。

表1　真空联合堆载预压处理后路基软土HS模型参数

基于标准三轴压缩试验实际尺寸直径为39.1 mm,高为80.0 mm建立数值验证模型,在设定初始围压下,施加轴向位移,记录试样顶部所施加的荷载。图5展示了数值三轴压缩试验中主应力差与轴向应变关系曲线及与实测数据的对比, HS模型参数很好地描述软土应力应变的非线性,直接推广到不同围压时同样能很好描述软土的非线性应力应变关系。

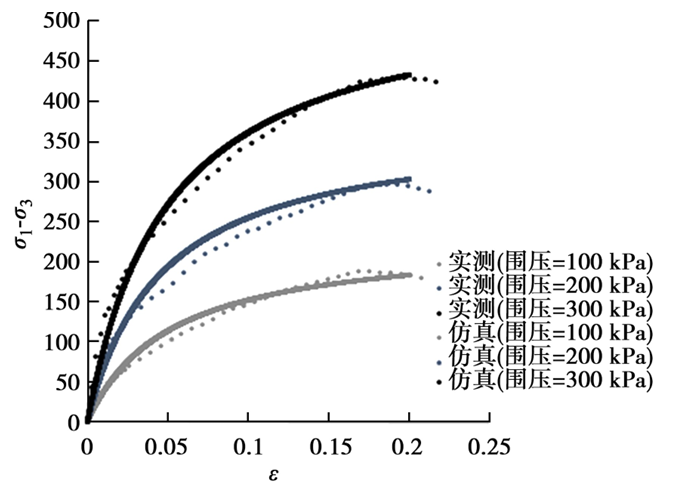
图5　数值和实测三轴压缩试验应力应变关系曲线对比

3　数值模型

3.1　几何模型

选取典型监测断面二(图2)进行平面应变分析,其支护剖面如图6,坑底被动区设置了7.2 m× 5.0 m的格栅式水泥土搅拌桩加固。软黏土和极软弱黏土的沉降影响范围能到2~4倍开挖深度,在较厚深度的软黏土中甚至能超过4倍开挖深度,为减小边界影响,几何模型按照侧边界离开挖边线按不小于5倍基坑开挖深度设置,并适当包含路基侧未处理软土部分,坑底边界按桩底和相对硬土层控制。土层分布按照第二监测断面钻孔显示地层设置,如图7。

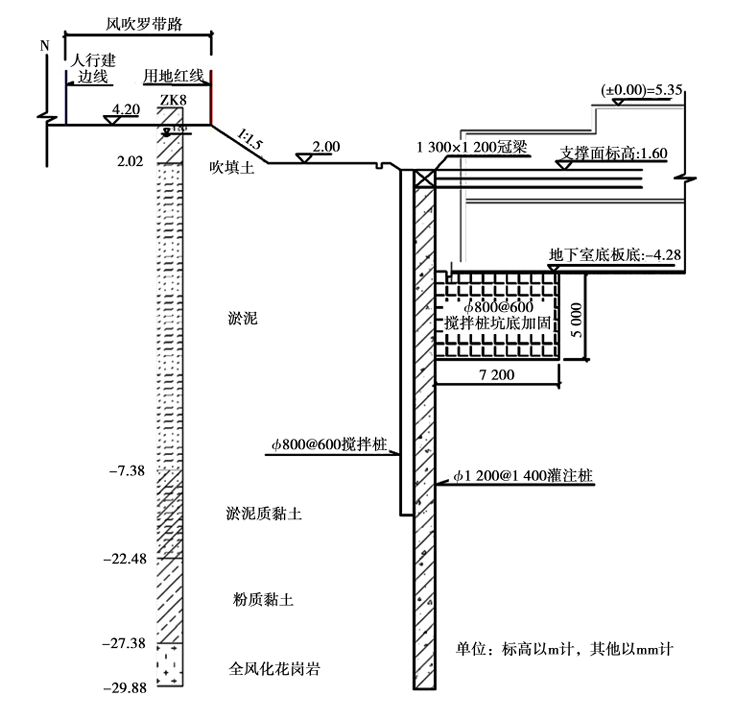
图6　监测断面二处支护剖面示意

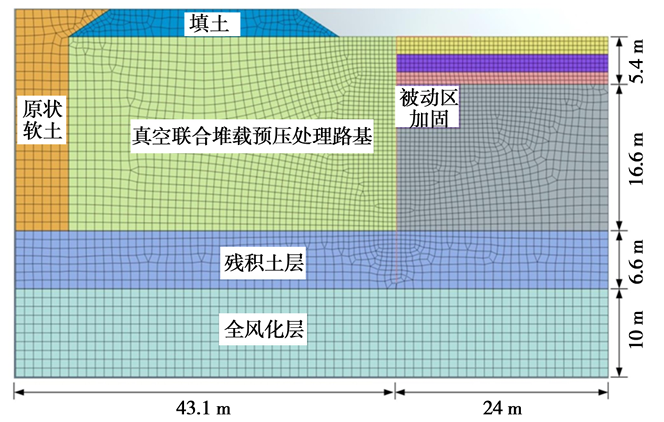
图7　有限元模型及网格划分

土体采用平面应变二维网格;基坑围护结构的桩采用梁单元,按等效刚度原则高度取0.955 m,宽度取单位宽度1 m。内支撑设置根据等刚度原则确定水平支撑的长度为8.5 m,宽×高分别为0.4 m×0.15 m。

对支护结构附近网格进行加密处理,最终划分的有限元网格模型如图8。边界条件设置为位移边界条件,模型底部固定,两侧法向固定。

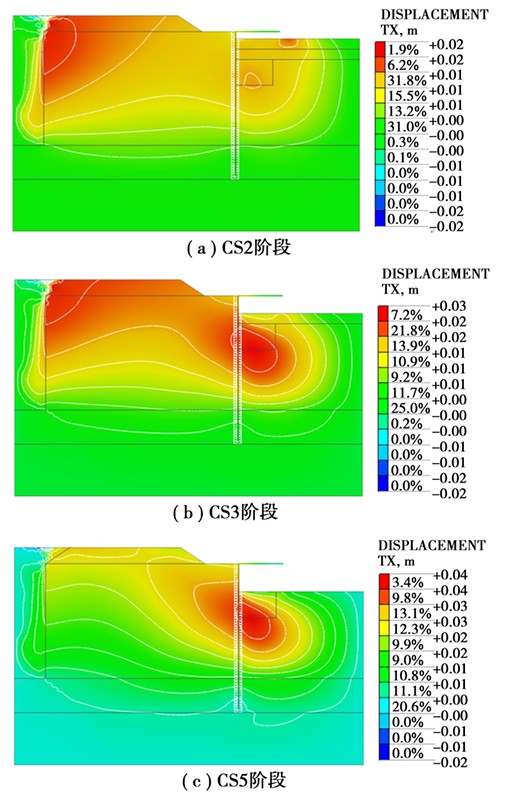
图8　水平位移云图

3.2　施工工况与物理力学参数

软土路基在基坑施工开挖第一、二阶段封闭,无施工荷载,原状软土处的堆载按10 kPa设置;开挖第二阶段结束后有车辆及建筑材料堆放,均布活载取15 kPa。数值模拟根据实际施工阶段设置5个计算步,具体见表2。根据项目详细勘察阶段成果和实验室试验结果,土层模型及相关物理力学参数指标汇总于表3,其中基坑施工前对坑内软土进行了堆载排水处理,物理力学参数与处理后软土路基参数相同。桩土界面摩擦强度与周围土层相同,法向刚度和剪切按程序默认设置。被动区水泥土搅拌桩置换率m=0.54,水泥土无侧限抗压强度qu=0. 6 MPa,取水泥土的变形模量E= 100 qu,按照加固土体复合模量的计算方法,坑底加固土体的复合模量E=29.0 MPa。同样地,取水泥土的黏聚力和内摩擦角分别为148 kPa和20°,计算出坑底加固土的复合黏聚力和内摩擦角分别为71.9 kPa和11.1°。

表2　计算步与施工工况的对应

表3　物理力学参数指标

数值分析中的基本假定:

(1)基坑施工时间段,设计支护桩外层布设了直径为800 mm的搅拌桩止水帷幕并深入黏土层,同时淤泥层渗透性低,因此不考虑土体的排水固结,按不排水条件进行总应力分析。

(2)不考虑温度、时空效应影响。

4　数值模拟及实测结果分析

4.1　路基深层水平位移分析

图8为基坑开挖影响下的软土路基水平位移云图。CS2阶段(图8(a)):围护结构施工与坑内第一层土开挖所引起的水平位移最大值为19.1 mm(按朝基坑内描述为正值),出现在路基原状软土侧,原状软土为流塑状,在堆载作用下对路基产生较大的侧向力,致使路基发生较大变形;第一层土开挖同样也引起了路基的侧向变形,但因为支护桩的约束,对路基水平位移影响小于原状软土,基坑壁水平位移。CS3阶段(图8(b)):坑内第二层土开挖所引起的路基水平位移最大值为26.1 mm,出现在开挖面以下,随着坑内土体的开挖,基坑开挖卸荷对路基水平位移的影响变得显著,路基出现整体向坑内移动的趋势。CS5阶段(图8(c)):坑内第三层土开挖所引起的路基水平位移最大值为40.5 mm,出现在开挖面附近,水平位移云图上展现了明显的基坑开挖影响线。

软土路基侧原状软土上的堆载会传递到路基,致使路基发生侧向变形,叠加基坑开挖卸荷的影响,会出现路基整体向坑内移动趋势。随基坑开挖深度的增加,基坑开挖卸荷对路基水平位移的影响愈发明显,其水平位移最大值慢慢发展至开挖面附近,路基整体呈现鼓出形状。

4.2　路基表面沉降规律分析

图9为基坑开挖影响下的地层竖向位移云图,可以看到基坑侧路基表现为下沉,坑底位置表现为隆起。CS2阶段(图9(a)):路基侧原状软土区域堆载引起原状软土沉降达到了-110 mm,围护结构施工与坑内第一层土开挖所引起的路基沉降较小,同时坑底隆起量最大值为60.86 mm。CS3阶段(图9(b)):坑内第二层土开挖使得路侧原状软土区域沉降达到了-129.53 mm,引起路基沉降最大值为-3.2 mm,出现在近基坑侧;坑底隆起量最大值为134.71 mm。CS5阶段(图9(c)):路基顶施加活载15 kPa和坑内第三层土开挖使得路侧原状软土区域沉降达到了-134.7 mm,所引起的路基沉降最大值为-30.3 mm,出现在路侧原状软土区域;坑底隆起量最大值为194.0 mm。基坑的开挖卸荷会持续扰动路侧原状软土区域使沉降增大,而随基坑开挖深度的增加,对路基沉降的影响越明显。

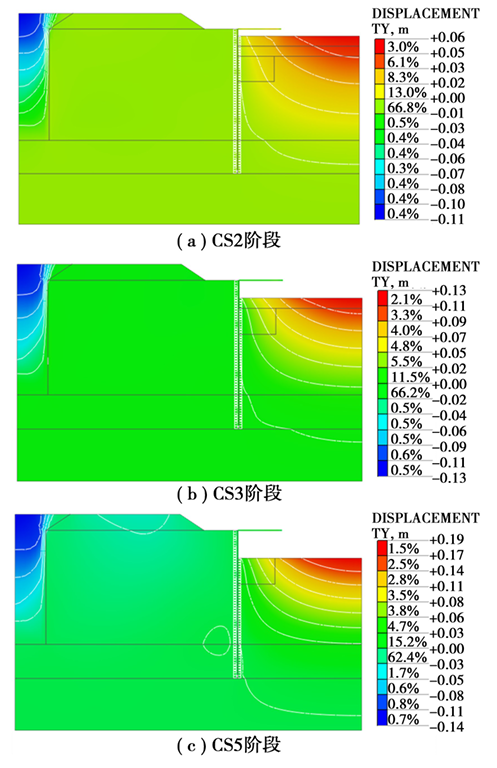
图9　竖向位移云图

基坑开挖影响下的路基表面沉降变化规律如图10所示,路基沉降呈现凹形沉降槽,其中距路基顶距离为0m的位置即为靠基坑侧路基顶。 CS2阶段:由坑内第一层土开挖引起的路基沉降最大值为-1.3mm,变形趋势呈三角形;CS3阶段:坑内第二层土开挖引起路基累计沉降最大值为-6.2mm; CS4 阶段:路基顶施加均布活载引起路基累计沉降最大值为-25.8mm;CS5阶段:坑内第三层土开挖引起路基累计沉降最大值为-30.3mm。

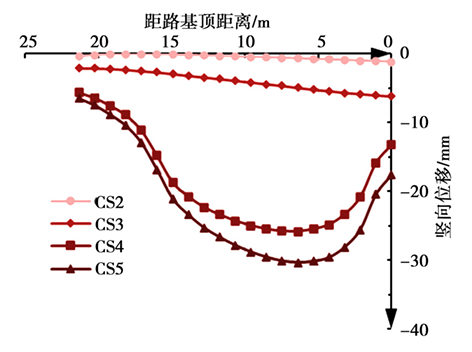
图10　基坑开挖影响下路基表面沉降规律

路基顶面的均布活载引起路基沉降达到了-19. 5mm,占到了累计沉降量的64.4%,路基顶面的均布荷载是引起路基沉降的主要原因。 仅考虑基坑开挖引起的路基沉降约为-11.0mm,路基表面沉降呈凹槽型,影响范围为整个路基,超过5倍基坑开挖深度,在路基上面的建筑材料、车辆等的堆载会引起路基的明显沉降,最终路基累计沉降量达到了-30.3mm。

4. 3　数值计算与实测结果对比分析

根据设置在监测断面二上的两个深层水平位移监测所处位置,提取数值分析计算中相同位置的土体深层水平位移,对两者在相同阶段的深层水平位移进行对比分析。 图11(a)和11(b)分别为监测断面二CX2-1(距坑边21.5m)和 CX2-2(距坑边11.2m)处土体深层水平位移现场实测与数值计算结果。

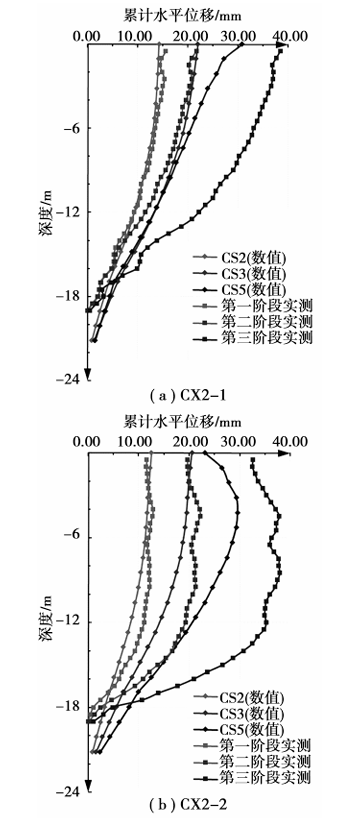
图11　路基深层水平位移对比

基坑开挖第一阶段:CX2-1实测深层水平位移最大值为15.6mm,变形趋势表现为测斜孔向坑内倾斜; CX2-2 实测深层水平位移最大值为12.8 mm,最大位移出现在土体深层。第二阶段: CX2-1实测深层水平位移最大值为21.7 mm,变形趋势同样向坑内倾斜;CX2-2实测深层水平位移最大值为22.2 mm,最大位移出现在土体深层。

第一阶段和第二阶段数值计算结果与实测深层水平位移的变形趋势和数值基本接近。因路侧原状软土强度低,以及原状软土上的堆载,导致第一阶段远离基坑侧的CX2-1深层水平位移大于CX2-2,随着开挖深度的增大,基坑卸荷效应增强,近基坑侧的CX2-2深层水平位移逐渐大于CX2-1。

第三阶段数值计算结果与实测深层水平位移变形趋势相同,由于内支撑在坑顶的约束作用,近基坑侧路基深层水平位移最大值都出现在开挖坑底附近,路基整体呈现鼓出形状。远基坑侧变形趋势与第一、二阶段相同,表现为向坑内倾斜;第三阶段数值计算结果明显偏小,深层水平位移实测值为坑内底板施作完成后的值,实测过程在基坑开挖到底至底板施工完成,深层水平位移实测值在不断地发展变大,而数值分析计算至基坑开挖到底即认为变形稳定,并没有考虑流变等时间和空间效应。真空堆载联合处理后软土路基在侧向卸荷和路侧软土挤压共同作用下,会发生显著的蠕变效应,表现为路基深层水平位移会不断发展,因此在开挖至坑底后,应及时施作底板,以控制路基的过大变形。

5　结论

(1)真空联合堆载预压处理后软土路基在路侧原状软土侧向压力下,发生远基坑侧深层水平位移大于近基坑侧的情况,而随基坑开挖加深的持续影响,近基坑侧水平位移会迅速发展。远基坑侧水平位移表现为倾斜,而因内支撑在坑顶的约束作用,近基坑侧水平位移表现为开挖面附近的“鼓出”。

(2)真空联合堆载预压处理后软土路基表面的沉降同时受路面荷载和基坑开挖卸荷影响,路面沉降的控制应综合考虑路面荷载和开挖卸荷。

(3)基坑开挖第一阶段和第二阶段数值计算和实测结果吻合度高;路侧原状软土侧向压力下,受软土的流变影响,深层水平位移会不断发展,开挖第三阶段实测值显著大于数值计算,因此在开挖至坑底后,应及时施作底板,以控制路基变形的发展。