0 引言
在我国隧道建设如火如荼的大背景下,盾构隧道的管片预制化和机械化拼装优势使其得到了广泛的应用。 但是由于盾构管片接头的刚度较为薄弱,且具有复杂接触状态及非线性力学特征,因此盾构管片接头状态将会直接影响到隧道结构整体稳定性。 尤其是在隧道长期服役过程中,某些结构缺陷、复杂荷载作用、螺栓预应力损失等多重隐患共同作用下,盾构管片接头将出现不同程度的损伤,并直接导致盾构隧道结构整体出现收敛变形。 当接缝张开过大时,地铁隧道的收敛变形也会产生极大的变化,尤其对于大断面盾构隧道,收敛变形已经成为影响地铁正常运营的重要因素。 收敛变形指标不但可以直观反映盾构隧道结构整体服役状况,而且与管片应力应变等其他指标相比更加准确且容易测得,因此,收敛变形逐渐成为评价盾构隧道结构整体稳定性的关键指标。
目前不少学者从模型试验和数值模拟等方面对盾构隧道接缝张开和收敛变形进行了研究。 陈枰良等基于正接触非线性力学模型推导出了一种新的接缝张开量计算方法。 张稳军等研究了地震强度对管片变形的影响。 郑刚等通过试验研究了不同管片张开量下的水土流失规律。 殷剑光等针对螺栓锈蚀对接头性能的弱化作用开展了系统研究,并明确了螺栓锈蚀与接头变形及结构稳定性之间的关系。 章登精等提出了不同变形模式下的收敛标准。 邱月等基于原型弧形接缝结构加载试验分析了破坏程度与接缝变形的关联。 李晓军等通过正负弯矩荷载试验分析了接缝张开量变化规律。 张稳军等、卢院等、林伟波等、张金红等研究了衬砌收敛变形与病害统计特征之间的关系。
为了解隧道结构运营期力学行为演化规律,实现对隧道健康状况的实时感知,近年来结构健康监测系统逐渐应用到隧道中。 本文以南京扬子江隧道为依托工程,基于现场接缝张开度的健康监测数据,建立单环管片精细化数值模型,以监测数据对比验证数值模型的准确性与可行性,并通过该数值模型研究纵缝张开与收敛变形的关系以及螺栓预紧力和管片拼装角度对收敛变形的影响,以期指导大断面盾构隧道的设计和施工。
1 隧道工程概况
南京扬子江隧道位于南京长江大桥与南京应天大街长江隧道之间,为“双管双层八车道”结构,隧道平面布置如图 1—2 所示。 隧道 N 线(北线)长 4 930 m,隧道 S 线(南线)长 5 530 m。 盾构隧道外径为 14. 5 m,内径 13. 3 m,厚度 0. 6 m,宽度2 m,采用错缝拼装。 每环管片由 1 个封顶块,2 个邻接块和 7 个标准块组成,管片各分块尺寸及各纵缝编号如图 3 所示。
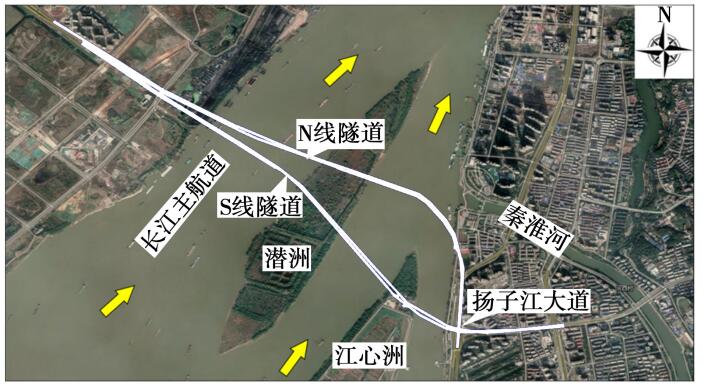
图 1 南京扬子江隧道平面示意图
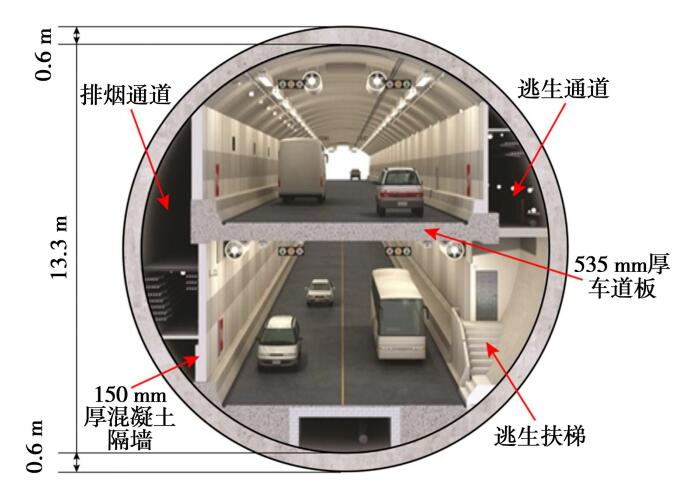
图 2 南京扬子江隧道断面内部结构
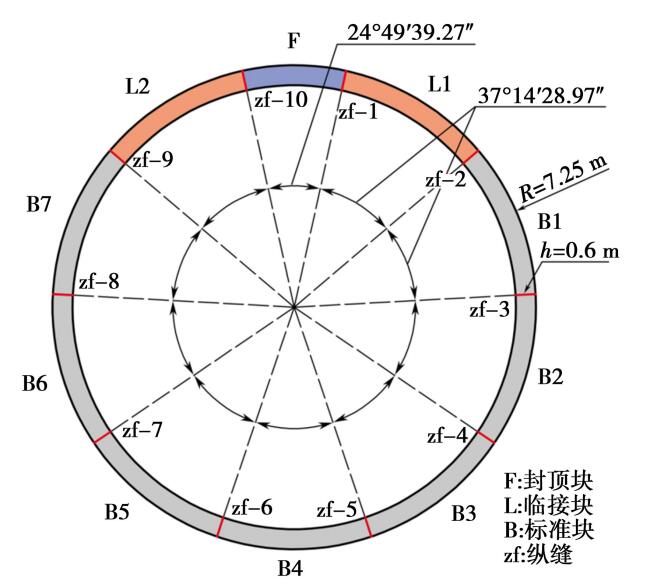
图 3 盾构管片拼装形式及纵缝编号
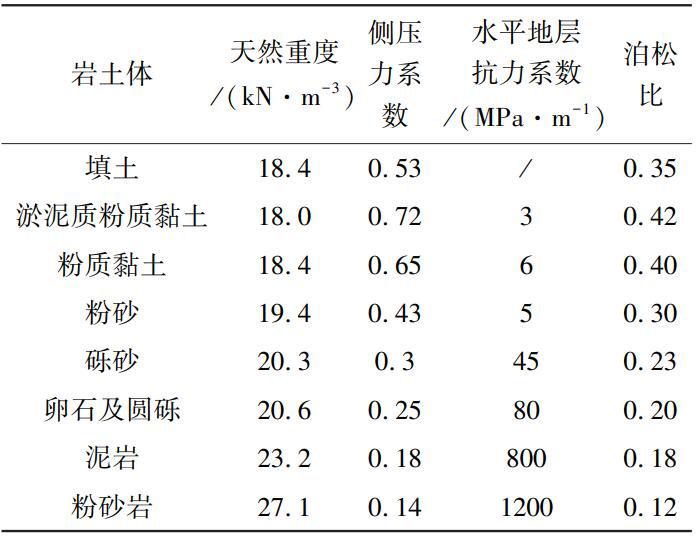
盾构隧道主要穿越粉质黏土、粉砂、淤泥质粉质黏土、砾砂、圆砾及卵石、中风化粉砂岩等地层,主要的岩土力学参数如表 1 所示。
表 1 岩土体力学参数
2 南京扬子江隧道管片纵缝监测方案
南京扬子江隧道结构健康监测系统于 2016 年6 月正式上线。 本文选取 2016 年 6 月 4 日至 2016年 11 月 30 日期间 3 个典型断面共 6 个月的监测数据进行分析,全线各断面位置如图 4 所示。
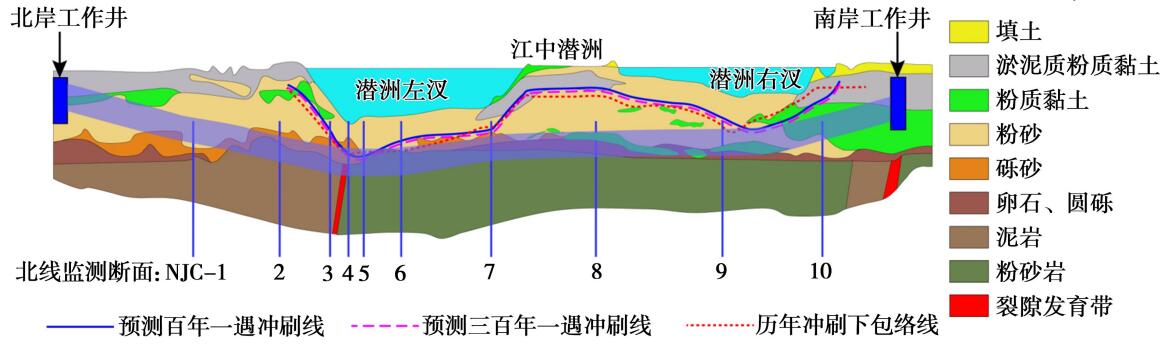
图 4 N 线主监测断面纵剖图
此处选取的 3 个典型断面为 NJC-4、NJC-6、NJC-8。 其中,NJC-4 断面位于潜洲左汊江水最深处,为全线覆土最浅、水头最高处,且隧道穿越多种地层的交界面。 NJC-6 断面位于潜洲左汊江心位置,江水较深,全断面穿越粉砂岩单一地层。 NJC-8断面位于江心洲下方,全线覆土最厚,穿越粉质黏土、卵石、粉砂岩地层。 在隧道贯通后,将测缝计跨越管片锚固安装于纵向或横向接缝两侧,各断面纵缝接缝计的安装位置如图 5 所示。 测缝计使用北京基康仪器股份有限公司的 BGK-FBG-4420T 型测缝计,安装时将测缝计跨越管片锚固安装于纵向或横向接缝两侧,如图 6 所示。
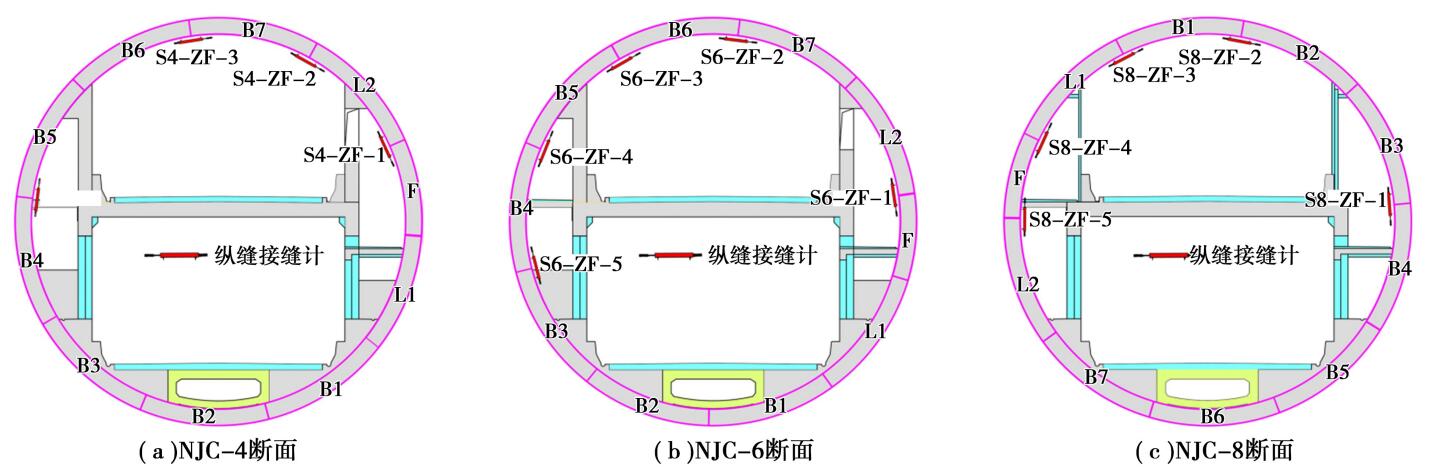
图 5 各断面纵缝接缝计位置

图 6 纵向测缝计现场安装照片
3 单环管片三维数值模型
首先采用 Rhino 三维建模软件按照真实尺寸和管片分块方案进行建模,再导入有限元计算软件中进行参数赋值、荷载定义、边界条件、网格划分等操作。 由于密封橡胶垫一般在接缝防水中发挥作用,对于管片接头性能的影响很小,接触面的主要受力部分为接缝处混凝土和螺栓,因此忽略密封橡胶垫的建模,模型中也未考虑吊装孔及手孔的影响。 本文所建立的数值模型如图 7 所示。
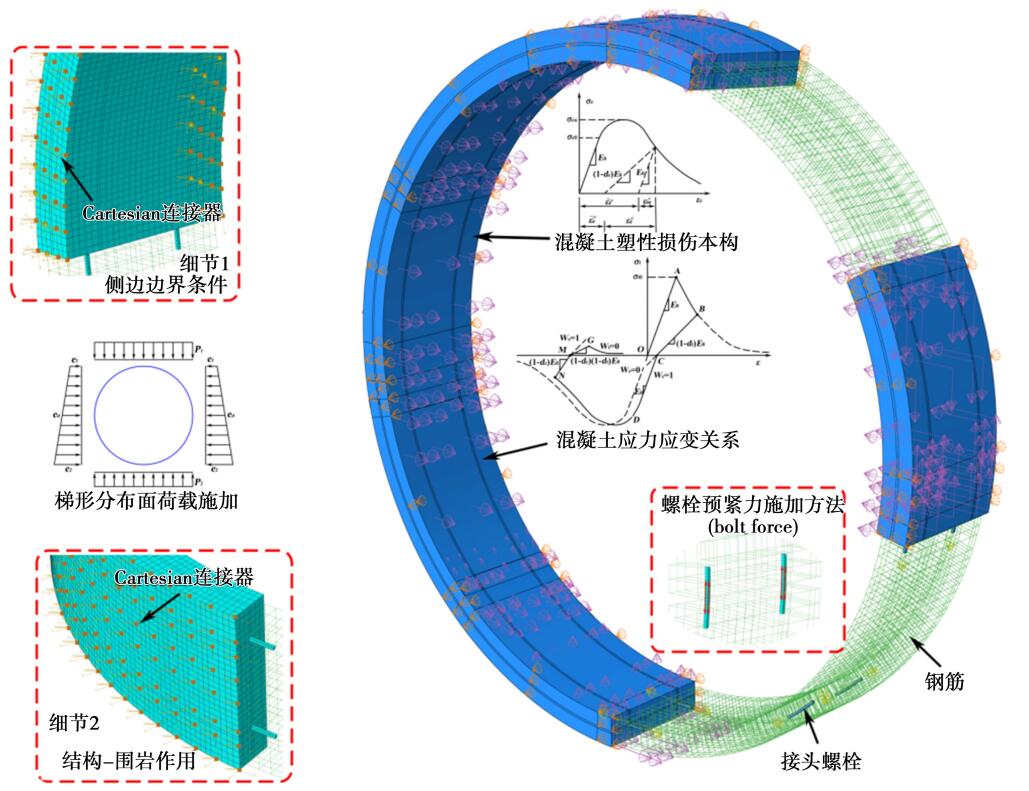
图 7 三维数值模型示意图
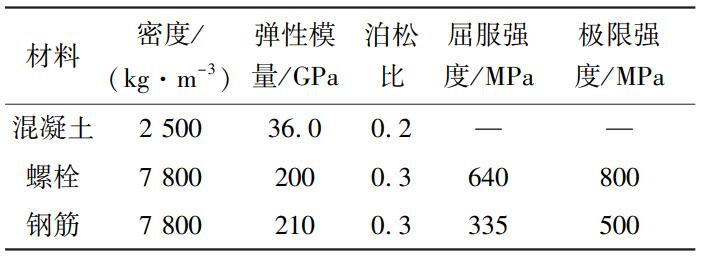
管片混凝土等级为 C60, 环 向 主 筋 规 格 为HRB335,纵缝接头处为 2 根 8. 8 级 M36 环向螺栓。 具体材料参数如表 2 所示。 其中模型中混凝土弹性模量要考虑管片手孔、吊装孔等引起的刚度折减,参考相关研究取折减系数为 0. 85。
表 2 材料属性参数
网格划分时,管片和螺栓均采用三维六面体八节点实体单元(C3D8R),钢筋则采用三维两节点杆单元(T3D2),并将钢筋单元嵌入(Embedded)混凝土单元中,以此模拟钢筋对管片的加强作用,不考虑钢筋与混凝土在交界面上的粘结滑移。
混凝土材料采用塑性损伤本构进行表征,其中损伤因子采用 Sidoroff 能量等效原理进行计算,详细参数如表 3 所示。 螺栓和钢筋均采用双直线弹塑性本构。
表 3 混凝土塑性损伤参数

模型纵缝处的管片与管片之间、螺栓孔与螺栓之间均采用面 面接触,其中法向为“硬接触” 模式,切向采用 Oden 等[26]提出的摩擦系数随滑移速率的指数衰减模型,如式(1)所示:
μ = μk+ (μs- μk )e-dcγ·eq (1)
式中: μk 为 滑 动 时 接 触 面 的 动 摩 擦 系 数, 取0. 453;μs 为静摩擦系数,取 0. 6;dc 为折减系数,取 5. 56;γ·eq 为滑动速率(mm / s)。
模型中在螺栓与接缝面交汇处施加预紧力,按照设计要求,8. 8 级 M36 高强螺栓预紧力为 280 kN。
土与隧道结构的相互作用通过 Cartesian 连接器(Wires to ground)来实现。 径向约束为受压不抗拉的非线性弹簧。 地层抗力系数依据封坤等提出的地层抗力系数修正计算方法进行计算,如式(2)—(3)所示。 与现有计算方法相比,该方法提出了针对荷载分布和断面位置的修正系数,弥补了以往全断面地层抗力系数单一取值的不足。
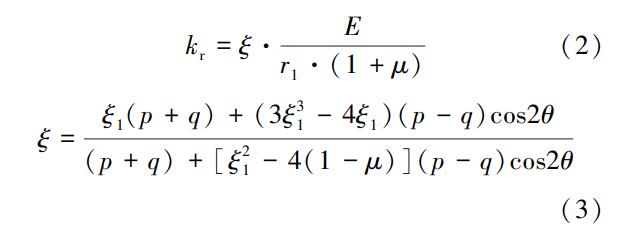
式中:E、μ 分别为地层的变形模量和泊松比;p 为竖向压力;q 为水平侧压力;ξ1= r1/ r,为地层抗力计算点位置 r 与隧道开挖半径 r1 之比,当 r = r1 即ξ1= 1 时为计算隧道周边地层抗力;ξ 为与地层荷载 p、q 及断面位置 θ 有关的修正系数,。
单环管片还受到相邻环管片的挟持作用,为了准确模拟单环管片的受力情况,必须考虑模型中管片的侧面边界条件。 垂直于管片侧面的弹簧刚度通过何川提出的纵向等效抗弯刚度经过转化而来,侧面切向弹簧刚度依据肖时辉等提出的盾构隧道管片纵向连接侧面切向刚度计算公式求取。
4 接缝张开监测数据分析及数值模型有效性验证
由于隧道管片内力分布复杂较难测量,本文以纵缝张开量作为直接的可测量指标来衡量数值模型的有效性。 图 8—10 为上述 3 个断面测缝计监测数据,测缝计监测数据以 2016 年 6 月 4 日零时作为零点,之后监测数据均每隔 0. 5 d 读取一次,直至 2016 年 11 月 30 日零点时,个别仪器损坏导致部分监测数据缺失(图 6 中 S4-ZF-3)。
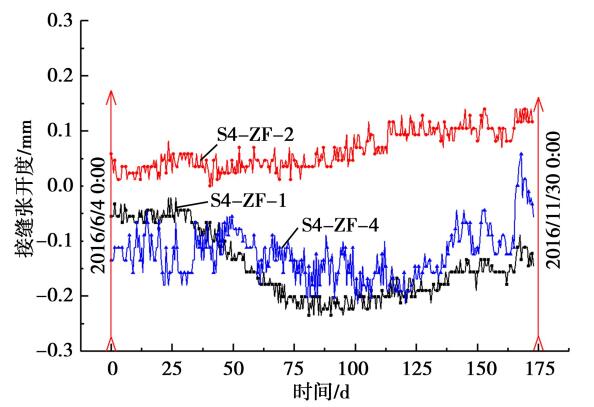
图 8 NJC-4 断面接缝张开度监测数据
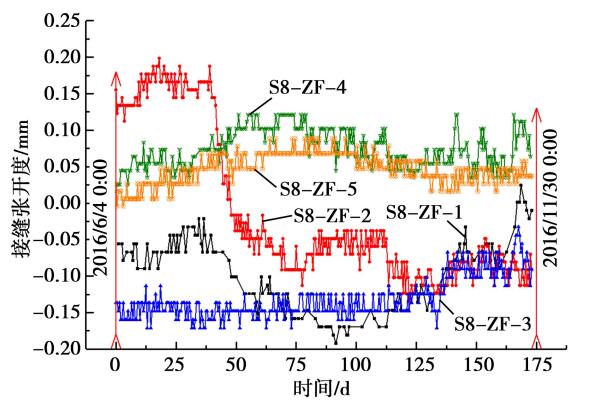
图 9 NJC-6 断面接缝张开度监测数据
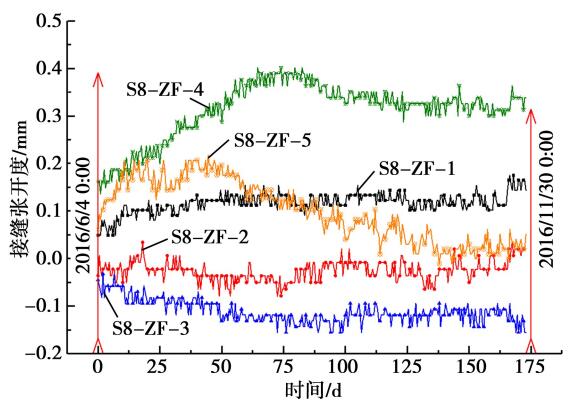
图 10 NJC-8 断面接缝张开度监测数据
从图中可以看出,在 6—11 月期间,纵缝绝对值变化趋势均为先增大后减小,该时期内正好经历了长江水位的上升与下降,这种纵缝变化现象主要原因可能为长江水位变化引起的隧道荷载变化。同时可以看出,对于透水地层的水下盾构隧道,设计水压力对衬砌结构安全的重要影响。
基于上述 3 个断面的工程土层分布条件、实际长江水位(参照长江海事局公布资料,取 6 个月的水位平均值) 并采用水土分算的方式计算衬砌荷载,荷载计算结果如图 11 所示,进行数值模型求解计算,提取管片环的接缝张开量。 对应位置监测值和模拟值的接缝张开量对比如表 4 所示。 表中各缝的监测值取 6 个月所有监测值得平均值。
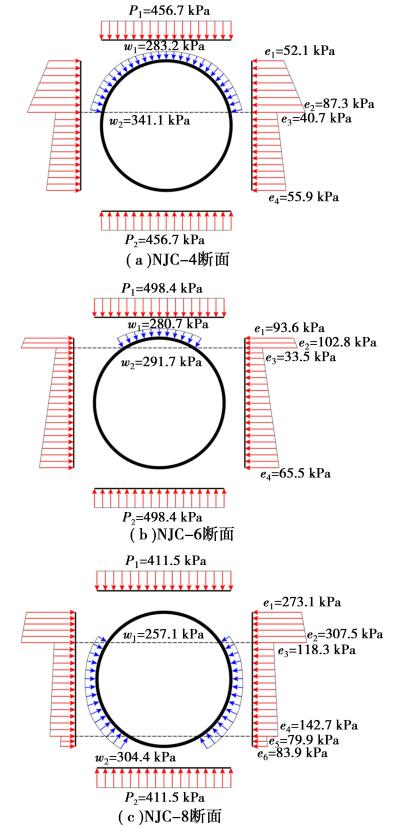
图 11 NJC-4/ 6 / 8 断面衬砌荷载
表 4 接缝张开量对比(单位:mm)
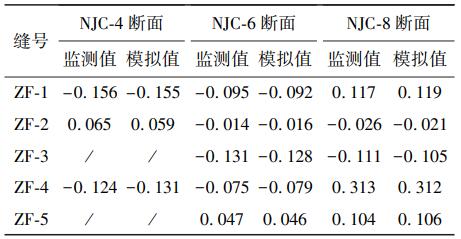
分析表 4 的监测数据可以看出,NJC-4 断面衬砌呈现“横鸭蛋” 变形模式,NJC-8 断面衬砌呈现“竖鸭蛋” 变形模式,NJC-6 断面衬砌呈现“圆状”变形模式,即 NJC-4 断面竖向荷载起主要作用,NJC-6 断面水平、竖向荷载作用均当,NJC-8 断面水平荷载起主要作用。
根据现场监测结果,从受力机理可作出以下解释:NJC-4 断面位于江水最深、覆土最浅处,1 / 2 下部断面下卧于粉砂岩地层,透水性差,地层抗力系数大,1 / 2 上部断面位于砾砂地层,透水性好,故可将隧道上半部分比作曲梁,在水压大、土压小的荷载作用下,使得隧道断面呈现“横鸭蛋”变形模式;NJC-6 断面虽然江水较深,但由于全断面位于粉砂岩地层,导致透水性差,故盾构隧道全环承受荷载的差异性较小,故管片各纵缝均有收缩且差距不大,断面椭圆度变化并不明显;NJC-8 断面位于江心洲下方,1 / 3 上部断面位于粉质黏土层,透水性差,地层抗力系数小,1 / 4 下部断面位于风化粉砂岩基岩层,地层抗力系数大,中间断面穿越卵石及圆砾层,透水性好,即该断面地下水性质为承压水,因此隧道拱腰部位的水平荷载较大,使得隧道呈现“竖鸭蛋”变形模式。
通过对接缝张开量的对比分析可以得出,仿真计算结果与监测结果较接近,一定程度上说明模型的建立和参数的选取是较为合理的,该模型可以应用于对收敛变形影响因素的计算分析。
5 收敛变形影响因素分析
5. 1 纵缝张开与收敛变形关系
本节假设隧道全断面位于圆砾及卵石全透水地层中,研究收敛变形的影响因素。 隧道收敛变形是外荷载作用下纵缝变形与管片自身变形两大主要因素共同作用的结果。 为了确定盾构隧道收敛变形的关键因素,本节进行了不同竖向荷载下的模拟计算。 以刚体管片环为对照模型(下文称之为刚体模型),忽略了管片的弯曲变形,由此可得到仅由管片绕纵缝刚体转动导致的收敛变形。 当管片采用实际刚度时(下文称之为实际刚度模型),可得到管片变形和纵缝变形共同导致的收敛变形。2 种模型的其他参数均相同,且均按第 3 节中的方法进行设置。 图 12 为纵缝张开导致的收敛变形占比变化曲线。
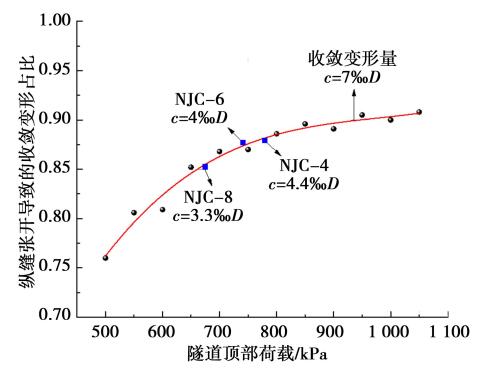
图 12 收敛变形占比变化曲线
从图 12 中可以看出,随拱腰收敛变形的增加,纵缝转动导致的收敛变形占比逐渐上升,因此纵缝张开是隧道环向发生收敛变形的关键因素,管片绕接缝处转动是收敛变形的主要形态。
当拱腰收敛变形达到 7‰D 以上时,纵缝张开导致的收敛变形在总收敛变形中的占比超过90%,且随收敛变形增加,占比逐渐增加。 因此,盲目提高管片刚度来减小拱腰收敛是不合理的。
5. 2 螺栓预紧力对收敛变形的影响
螺栓预紧力不足会导致管片纵缝转动刚度降低,间接影响隧道整体环向刚度。 为了量化螺栓预紧力对整体变形的影响程度,对螺栓施拧问题提出建议,本节进行了不同竖向荷载下的模拟计算,螺栓预紧力分别取 120 kN、200 kN、280 kN,以螺栓无预紧力为对照模型。 模型的其他参数均相同,且均按第 3 节中给出的方法进行设置。 图 13 为施加不同螺栓预紧力后收敛变形减小率变化曲线。
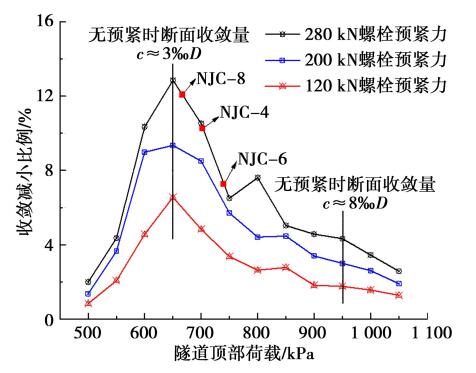
图 13 收敛变形减小率变化曲线
从图中可以看出,拱腰收敛变形 3‰D 左右时,施加螺栓预紧力效果接近峰值,螺栓预紧力越大,施加螺栓预紧力对拱腰收敛的控制效果越好。施加螺栓预紧力达到了一定的整体变形控制效果,但从现有的计算来看相对于无螺栓预紧力的情况减小率均不超过 15%,且随着拱腰收敛的增大,效果越来越不明显。 因此,对于大变形情况(>8‰D),施加并提高螺栓预紧力不建议成为控制收敛的主要手段。
5. 3 拼装角度对收敛变形的影响
为了考虑不同拼装角度对“收敛变形 纵缝张开关系”影响,现研究 4 种代表性拼装方式的拱腰收敛变形与拱顶内弧面纵缝张开关系,进行不同竖向荷载下的模拟计算,以便实际工作中根据容易测得的拱腰收敛变形,估计不易测得的拱顶纵缝张开情况。 4 种代表性拼装方式如图 14 所示,为 zf-1—zf-4 分别位于拱顶时对应的管片拼装情况。
图 14 4 种不同拼装方式模型
拱顶纵缝内弧面张开量随拱腰收敛变形的变化趋势如图 15 所示。 从图中可以看出,随拱腰收敛变形的增大,拱顶附近纵缝内弧面张开量增加,拱腰收敛变形与拱顶纵缝张开量的变化趋势基本同步。 在拱顶纵缝张开量相等的条件下,4 种拼装方式的拱腰收敛变形量排序为:a< b< c< d。
对所得数据进行拟合可得到 4 种典型隧道环拼装方式下拱顶纵缝内弧面张开量与拱腰收敛变形量的拟合公式,用于近似估算圆砾及卵石全透水地层中不同拱腰收敛变形下的纵缝张开量,其他地层可使用类似的方法进行研究。
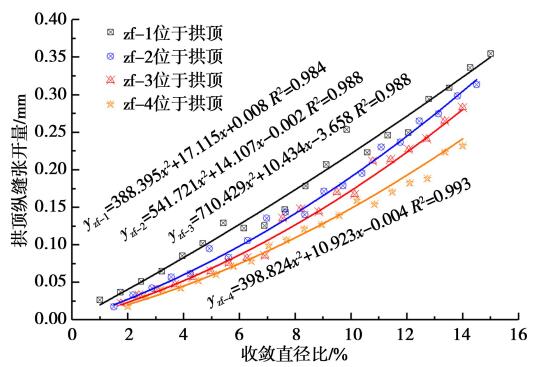
图 15 拱顶纵缝内弧面张开量随拱腰收敛变形量变化趋势
6 结论
(1) 本文建立的大断面水下盾构隧道单环精细化有限元计算模型与实测数据的吻合度较好,说明该模型可以反映不同条件下盾构隧道纵缝接头和整体断面的受力及变形规律。
(2) 纵缝张开是隧道环向发生收敛变形的关键因素,管片绕接缝处刚体转动是收敛变形的主要形态。
(3)增大螺栓预紧力能达到一定的收敛变形控制效果。 与大变形情况相比(>8‰D),小变形情况下提高螺栓预紧力对控制收敛的效果较好,因此不建议将提高螺栓预紧力作为控制收敛的主要手段。
(4) 得到了 4 种典型隧道环拼装方式下拱顶纵缝内弧面张开量与拱腰收敛变形量的拟合公式,可用于近似估算圆砾及卵石全透水地层中不同拱腰收敛变形下的拱顶纵缝张开量。
摘自《地下空间与工程学报 》