0 引言
近年来,随着城市地下空间的大规模开发利用,新建盾构穿越既有隧道工程频繁出现。 盾构穿越施工不可避免的会扰动既有隧道,引起其结构变形,甚至引发管片开裂、渗透水等病害。 这些病害不仅会在一定程度上给地铁运营带来安全隐患,严重时还会引发事故。 因此,研究盾构穿越对既有运营隧道的影响具有重要意义。
针对 该 问 题, 国 内 外 学 者 展 开 了 相 关 研究。 许多学者对下穿工程做了详细的实测分析。 但现场实测往往受到周围环境影响较大,不同工程由于地层条件、空间位置与施工措施等影响因素不同,既有隧道最终变形量与受影响范围存在差异。 现有的理论研究主要是基于 Winkler 弹性地基梁模型对隧道竖向变形进行求解,早期一般将地基反力考虑成一维弹簧模型作用,无法考虑应力的连续性。 近年来,虽然有学者引入更多参数对 Winkler 模型进行了修正,但引入更多参数后,修正模型计算复杂,参数确定困难。 且理论研究多是运用弹性模型,无法考虑塑性变形。
随着计算机技术和数值分析软件的发展,数值计算方法能真实、有效、经济地模拟各种工程及其施工过程,广泛用于穿越影响机理分析与工程影响因素评估。 陈越峰等通过三维有限元方法,得到盾构下穿施工时,既有隧道随盾构掘进发展的沉降规律及施工影响特点。 房明等、刘镇等结合广州地铁交叉隧道工程,改变复合地层类型,隧道覆土厚度,新旧隧道间距,施工参数及交叉角度进行数值模拟计算,从而得到不同工况下盾构施工对既有隧道沉降的影响。 刘树佳等运用数值模拟方法,得到新旧隧道间距,土仓压力及注浆量三者对既有隧道沉降的影响,并创新性的提出影响系数的概念。 何祥凡等针对上硬下软地层情况优化分析了掌子面顶推力。 丁智等采用三维有限元分析方法,在不同新旧隧道间距及角度工况下,分析了既有隧道变形和衬砌内力变化规律,并总结提出软土地区近接分区范围。 Lin 等对既有隧道纵向应力与横向扭转变形进行了深入研究,认为盾构下穿引起土体在既有隧道处产生土拱效应,使得既有隧道纵向受力发生偏移,并引起盾构正上方左右两侧既有隧道发生扭转。
虽然之前学者针对盾构穿越问题已进行了较多的研究,但大都聚焦于盾构推进对地层扰动规律和既有地铁变形的影响方面。 本文采用数值模拟方法,研究了不同竖向间距盾构下穿施工时隧道和地层的变形特性,以期揭示盾构下穿时新旧隧道间距对既有隧道变形机理及遮帘效应的影响规律。
1 三维数值模型
1. 1 数值模型
本文针对新建隧道与既有隧道正交的情况展开研究。 为了提高计算效率,考虑问题的对称特性,有限元模型取实际问题的一半。 地层沿新建隧道纵向的长度取 150 m,宽度取 100 m,高取 50 m,如图 1 所示。 新建隧道正交下穿既有隧道,新建隧道和既有隧道直径均为 6 m,衬砌厚度均为 0. 3 m。新建隧道埋深为 30 m,既有隧道的埋深根据分析的工况进行调整。 模型单元数为 111 753 个,节点数为 181 816 个,如图 1 所示。 模型 4 个竖向面设置为水平约束,模型底面设置为三向约束,顶面为自由面。 土体和衬砌均采用实体单元模拟,盾构机采用板单元模拟。
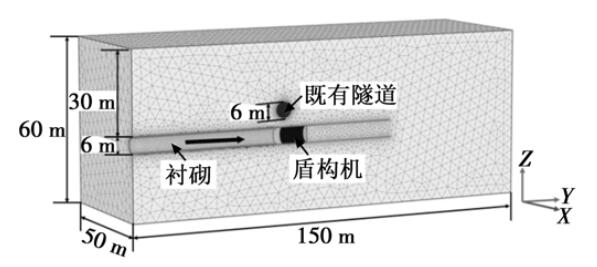
图 1 隧道正交下穿有限元计算模型
1. 2 计算参数选取
参考某实际工程,假设既有隧道和新建隧道都位于中粗砂层,为了更好的反应出盾构施工扰动对既 有 隧 道 的 影 响, 中 粗 砂 采 用 小 应 变 硬 化 模型( HSS 模型) 进行模拟。 对于砂性土,当土体的内摩擦角 φ>30°时,剪胀角 ψ 可取 φ-30°,另外,对于砂土,HSS 模型中四个刚度参数的关系可取 Eref50∶Erefoed ∶Erefur∶Gref0= 1 ∶ 1 ∶ 3 ∶ 5,刚度的应力相关幂指数 m 可取 0. 5,除此之外,本构模型中其它参数均通过室内试验与该工程的地勘报告确定。 如表1 所示。 由于隧道位于中粗砂中,隧道衬砌与其周围土体之间的接触面较为粗糙。 因此,在模型中反映界面单元刚度和抗剪强度降低的折减系数 Rint设置为 1. 0。
表 1 土体物理力学参数

盾构机和隧道衬砌采用线弹性本构模型,盾构机弹性模量为 230 GPa,泊松比为 0。 衬砌管片弹性模量为 31 GPa,泊松比为 0. 1。 考虑隧道衬砌环向和纵向接缝对刚度的削弱作用,环向衬砌的有效刚度取衬砌弹性模量的 0. 7 倍,在不考虑螺栓预紧力的情况下,纵向的有效刚度取衬砌弹性模量的 0. 1 倍。 即隧道衬砌的环向和纵向弹性模量实际取值为 21. 7 GPa 和 3. 1 GPa。
1. 3 盾构施工过程模拟
施工过程分为 2 个部分,先对既有隧道进行开挖。 通过冻结既有隧道区域的土体和激活该区域的衬砌来模拟既有隧道开挖。 既有隧道开挖完成后,将位移清零,再模拟新建隧道开挖的动态过程。假设盾构机一步一步向前推进,每次推进 3 m。 步骤一,冻结盾构机和注浆处土体,激活代表盾构机的板单元、开挖面处支护压力和作用于盾构机后方土体的注浆压力。 在模型中,设置盾构机的长度为9 m,采用盾构机前 6 m 区域模拟锥形盾壳和开挖引起的地层损失,在该区域内盾壳具有线性收缩,在盾 尾 处 收 缩 率 的 参 考 值 为 1% ( Cref ) , 增 量 为-0. 166 7% / m(Cinc ) 。 其余 3 m 长的区域用于模拟盾构机 尾 部,其 产 生 均 匀 收 缩,收 缩 率 为 1%。步骤二,冻结开挖面前方 3 m 的土体和之前的支护压力和注浆压力,激活当前开挖面的支护压力、步骤一中注浆处的衬砌和当前步骤相应位置的注浆压力来模拟盾构机的一次前进。 根据盾构机的施工参数,设置模型开挖面顶部支护力为 300 kPa,沿深度方向线性增加,梯度为 14 kPa / m。 盾尾顶部注浆压力为 330 kPa,沿深度方向线性增加,梯度为16. 8 kPa / m。 从新建隧道开挖面距既有隧道中心线 30 m 处开始模拟,到盾构机离开既有隧道 42 m处结束模拟。
2 有限元模拟结果分析
探讨新建隧道顶部与既有隧道底部间距 H 对既有隧道的影响,H 分别取 3 m(工况一) ,6 m( 工况二) ,9 m ( 工况三) ,12 m ( 工况四) ,15 m ( 工况五)和 18 m(工况六) ,如图 2 所示,无既有隧道为基准工况。
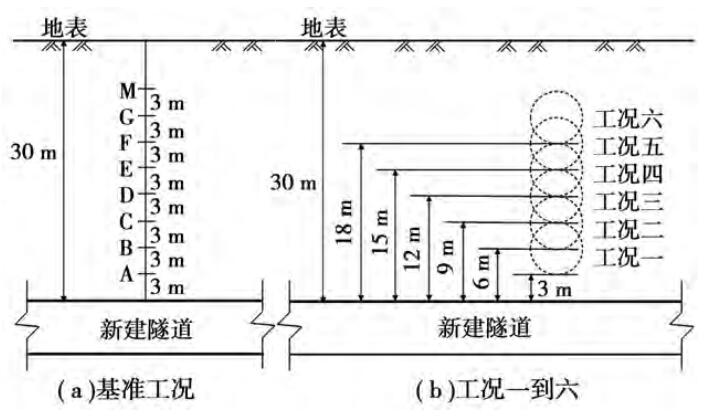
图 2 新建隧道与既有隧道位置关系
2. 1 既有隧道竖向位移分析
取基准工况八个点( ABCDEFGM) 与前六个工况进行对比。 由图 2 可知,工况一( H = 3 m) 中既有隧道底部与基准工况中 A 点位于同一位置,顶部与 C 点位于同一位置。 所以,A、B、C、D、E、F 共6 点分别距新建隧道顶部 3 m,6 m,9 m,12 m,15 m和 18 m,可与前 6 个工况的既有隧道底部进行对C、D、E、F、G、M 共 6 点分别距新建隧道顶部 9 m,12 m,15 m,18 m,21 m 和 24 m,可与前 6 个工况的既有隧道顶部进行对比。 L 表示盾构刀盘距既有隧道比,中心线的距离。
考虑到新建隧道与既有隧道是上下叠交关系,分析其受力特点可知,既有隧道受盾构施工影响主要为隆起或者沉降,故分析既有地铁隧道的竖向位移,如图 3 所示。 定义位移向上为正,向下为负。
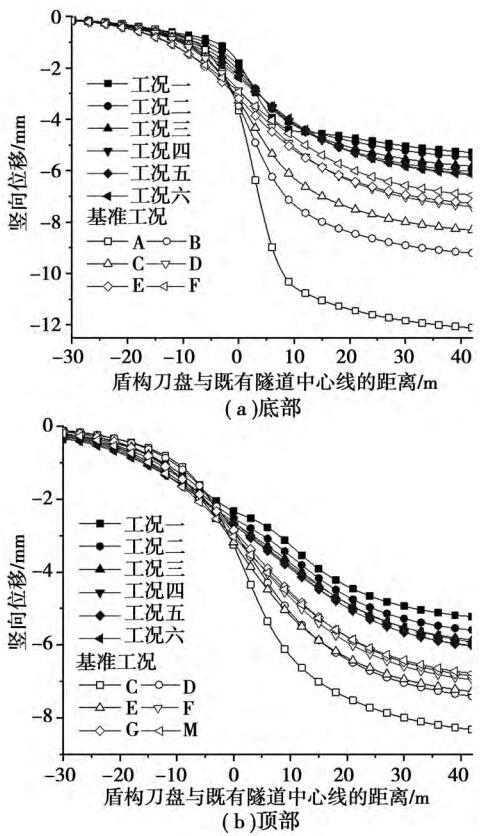
图 3 既有隧道竖向位移随盾构掘进的变化曲线
由图 3 可知,既有隧道顶部和底部均为沉降。这是因为下方隧道开挖应力释放,新开挖隧道拱顶移向临空面,进而带动上覆土层与既有隧道向下移动。 基准工况中,距离新建隧道越近,地层竖向沉降越大,即受盾构施工扰动越大。 在本文取的研究点中,A 点的最终沉降最大。 当盾构掘进面离 A点较远时,A 点竖向沉降较小,且变化缓慢;当掘进面距 A 点约 1D(D 为隧道直径) 位置时,A 点沉降变化量开始增大;当掘进面到达 A 点下方时,A 点沉降约达到总沉降的 30%;当掘进面通过 A 点约2D 位置时,A 点沉降完成约 90%。 其他各点与 A点竖向位移随掘进面位置呈现相似的变化规律,但在距 隧 道 ( 0. 5 ~ 1 ) D 内 地 层 的 沉 降 量 明 显 大于(1 ~ 4)D 部分。 由上述分析可知,地层的竖向位移主要在盾构掘进面前方 1D,后方 2D 和上方 1D范围内产生,建议下穿施工时需特别关注此段距离既有隧道的响应,必要时针对该区域进行局部加固处理,以确保运营地铁安全。
在上方有既有隧道的工况中,既有隧道顶底部与 A 点竖向位移随掘进面位置呈现相似的变化规律,但由于隧道和地层之间的刚度不同,隧道结构可以抵抗变形,既有隧道的竖向沉降小于基准工况中相同位置处的地层沉降。 由图 3 可知,在上方有既有隧道的工况中,工况一中既有隧道顶底部竖向沉降与基准工况中相同位置处的地层沉降相差最大,这是因为既有隧道与新建隧道之间间距越小,受新建隧道刚度的影响,限制既有隧道竖向变形能力越强,既有隧道沉降就越小。 新建隧道盾构施工对既有隧道的影响与隧 道 间 相 对 间 距 H 密 切 相关。 既有隧道竖向位移随间距 H 变化的趋势如图4 所示,取盾构刀盘与既有隧道中心线距离 L = 9 m和 L = 42 m 进行分析。
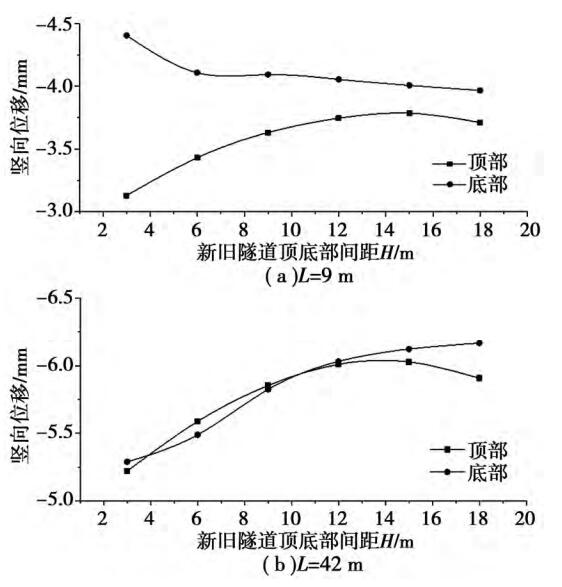
图 4 既有隧道竖向位移随 H 变化趋势
由图 4 可知,当 L = 9 m 时,随着间距增大,既有隧道顶部竖向位移先增加再趋于稳定,底部处竖向位移先减小再趋于稳定,且底部处竖向位移一直大于顶部处竖向位移。 这是因为此时盾构机掘进面刚通过既有隧道,既有隧道底部受到盾构施工扰动较大,且随着间距增加,盾构施工对既有隧道的扰动 逐 渐 减 弱,竖 向 位 移 逐 渐 减 小 并 趋 于 稳 定。当 L = 42 m 时,随着间距增大,既有隧道顶底部处竖向位移都是呈现出先增加再趋于稳定的趋势,且顶底部处竖向位移非常接近。 既有隧道竖向位移随间距 H 变化趋势与 L 有较大关系。
2. 2 既有隧道横断面管片收敛变形分析
由上述分析可知,新建隧道施工后,既有隧道顶底部处竖向位移非常接近,但不同工况下既有隧道顶底部竖向位移随掘进面位置的变化历程不同。在工况一到工况四中,既有隧道受新建隧道扰动最终顶底部竖向位移相同,而在工况五、六中,既有隧道最终顶部竖向位移小于底部竖向位移。 因此本文选择了工况一和工况六为对象,分析既有隧道顶底部竖向位移随盾构掘进的变化历程及既有隧道横截面变形,如图 5 所示。
由图 5( a)可知,在工况一中,当盾构掘进面离既有隧道中心线较远时,既有隧道顶部的竖向位移大于底部竖向位移,且差值较小;当掘进面距既有隧道中心线约 3D 位置时,既有隧道顶底部竖向位移差值开始增大;当掘进面到达既有隧道中心线下方时,既有隧道顶部的竖向位移仍大于底部竖向位移,但差值开始变小,直到掘进面通过既有隧道中心线约 1. 5 m( 0. 25D) 位置时,既有隧道顶底部的竖向位移相等,且之后开始呈现出顶部竖向位移小于底部的趋势。 当盾构掘进面通过既有隧道中心线(0. 25 ~ 1. 5) D 位置时,既有隧道顶部的竖向位移小于底部竖向位移,且差值逐渐增大;当掘进面通过既有隧道中心线 1. 5D 时,既有隧道顶部的竖向位移仍小于底部竖向位移,但差值开始变小,直到掘进面通过既有隧道中心线约 4D 位置时,既有隧道顶底部的竖向位移趋于相等,这是因为盾构掘进时对前方土体的扰动影响范围的边界线与水平线有一定的夹角,所以当掘进面距离既有隧道很远时,既有隧道顶部处受到扰动更大。 当盾构掘进面到达既有隧道下方时,整个既有隧道位于盾构扰动区,此时因为底部距离新建隧道近,受扰动更大,所以底部沉降大于顶部沉降。 同时由图 5( a) 可知,当 L = 12 m 时,既有隧道底部沉降变化量突然变小,这是因为既有隧道与新建隧道间距太小,注浆压力带来的抬升作用。 当盾构已经掘进完成后,顶底部处竖向位移非常接近。 这是因为既有隧道刚度相对较大,呈现出刚体变形特点。 鉴于隧道沉降经历了 3 个阶段,现选取 3 个不同阶段时刻既有隧道横截面的变形状态(即,L = -9 m,L = 9 m 和 L =30 m)进行分析,如图 5( a)所示。 随着新建隧道盾构掘进,既有隧道横截面变形逐渐增大,开挖过程中,既有隧道横截面先出现斜“鸭蛋” 变形,再变为竖“鸭蛋”型,终变为斜“鸭蛋”变形。
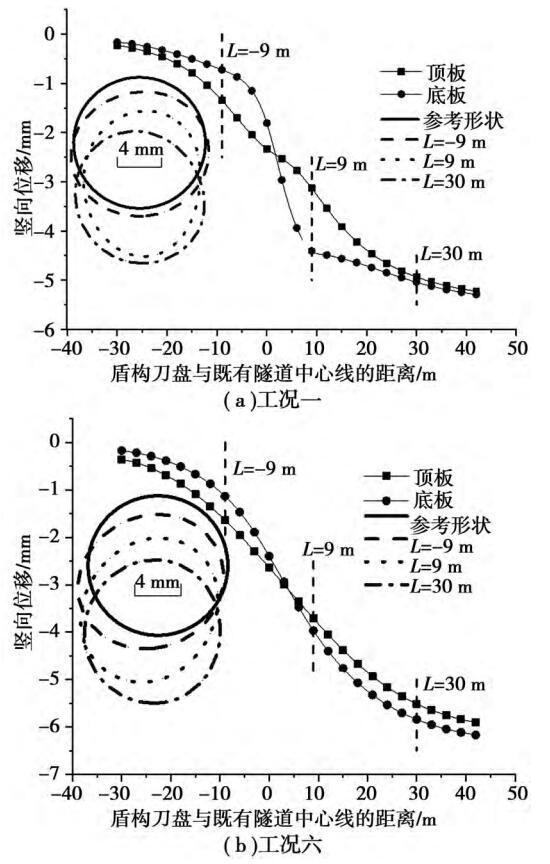
图 5 既有隧道竖向位移及横截面变形(放大系数 F = 500)
同样的,由图 5( b) 可知,在工况六中,随着盾构掘进,既有隧道的顶部竖向位移先是大于底部竖向位移,最终发展为小于底部竖向位移。 原因与工况一相同。 选取 3 个不同时刻的既有隧道横截面变形状态,分别是 L = -9 m,L = 9 m 和 L = 30 m。 随着新建隧道盾构掘进,既有隧道横截面变形逐渐增大,开挖过程中,既有隧道横截面先出现斜“鸭蛋”变形,终变为竖“鸭蛋” 型。 由上述分析可知,在工况一到工况四中,即 H<2D(12 m)时,既有隧道的顶部竖向位移最终发展为等于底部竖向位移,既有隧道横截面出现斜“鸭蛋”变形;在工况五、六中,即 H>2D 时,既有隧道的顶部竖向位移最终发展为小于底部竖向位移,既有隧道横截面出现竖“鸭蛋”变形。
工程中经常采用隧道横截面的收敛变形来评价盾 构 管 片 的 受 力 状 态, 下 面 本 文 将 引 入 椭 圆度(圆形隧道管片衬砌拼装成环后隧道最大与最小直径的差值与隧道设计内径的比值,以千分比表示)概念,探讨不同间距盾构下穿对既有隧道最大椭圆度的影响,如图 6 所示。
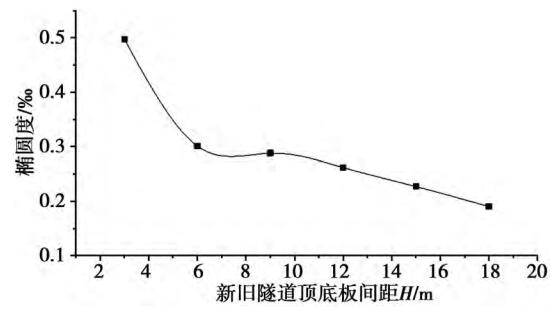
图 6 既有隧道最大椭圆度随 H 变化趋势
由图 6 可知,既有隧道最大椭圆度随间距 H增大而减小,间距越小时,既有隧道受到的扰动越大,横截面变形越明显。 虽然椭圆度值均在规范要求控制的 3‰范围内,且盾构上方( 0. 5 ~ 3) D 内最大椭圆度的变化规律相同,但(0. 5 ~ 1)D 内椭圆度变化量明显大于( 1 ~ 3) D 部分,故间距在 1D 范围内时,盾构施工需加强安全意识。
2. 3 地层竖向位移
图 7 为受新建隧道影响,既有隧道中心线处地层随深度发展的竖向位移曲线。

图 7 隧道中心线处地层随深度发展的竖向位移曲线
如图 7 所示,在基准工况中,虽然盾构上方地层均是随埋深沉降逐渐增大,但 2D 内地层沉降随深度产生了急剧增加,表明在盾构上方 2D 范围内地层之间产生了相互分离,即地层处于松散状态。而在盾构上方(2 ~ 4)D 范围内地层沉降缓慢增加,表明在该区间范围内的地层发生了整体沉降。 对比前 6 个工况,易发现工况一、二的既有隧道与新建隧道中间的地层沉降量随深度急剧增加,既有隧道位于松动区,此时既有地下结构可能因新隧道开挖产生的沉降超过设计允许值,甚至导致混凝土管片开裂,因此需要采取必要的加固措施。
如图 7 所示,在 6 个工况中,既有隧道上方地层竖向位移缓慢变化,且出现了先增加后减小的趋势,即隧道上方的地层最大沉降处位置距既有隧道顶部仍有一定距离。 这是因为既有隧道的刚度远大于地层,下方盾构扰动引发地层变形时,既有隧道上方 一 定 范 围 内 地 层 的 沉 降 较 小 ( 如 图 8 所示) ,体现为既有隧道的遮帘作用。 遮帘距离随间距变化如图 9 所示。
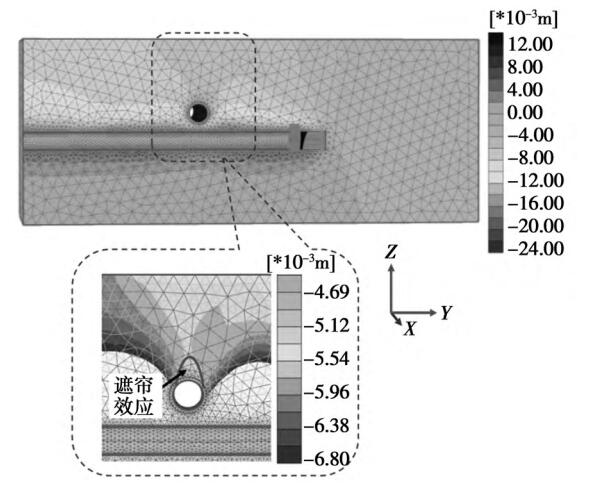
图 8 既有隧道遮帘效应对上方地层的影响
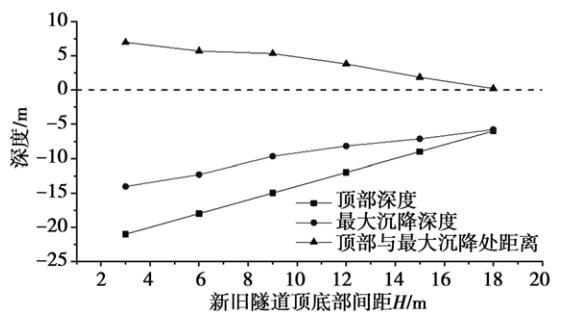
图 9 既有隧道顶部与最大竖向位移处距离随 H 变化趋势
如图 9 所示,遮帘距离随间距的增加而减小,即随着间距的增加,新建隧道对既有隧道的影响逐渐变小。 易知,随着新旧隧道间距的增大,遮帘效应影响程度随之减小,上方地层最大沉降处到既有隧道顶部距离减少。
3 结论
(1)基准工况(无既有隧道)中,地层的竖向位移主要在盾构掘进面前方 1D,后方 2D 和上方 1D范围内产生。 下穿工况中,既有隧道的竖向沉降小于基准工况中相同位置处的地层沉降。
(2)不同 间 距 下 既 有 隧 道 横 截 面 变 形 不 同。当间距小于 2D 时,既有隧道顶部竖向位移最终发展为等于底部竖向位移,既有隧道横截面出现斜“鸭蛋”变形;当间距大于 2D 时,既有隧道的顶部竖向位移最终发展为小于底部竖向位移,既有隧道横截面出现竖“鸭蛋”变形。
(3)既有隧道最大椭圆度随间距 H 增大而减小,椭圆度值均在规范控制的 3‰范围内。 但盾构上方(0. 5 ~ 1) D 内椭圆度变化量明显大于( 1 ~ 3)D 部分,故在 1D 范围内盾构 施 工 仍 需 加 强 安 全意识。
(4)既有隧道与新建隧道之间间距越近,之间的地层沉降随深度变化速度越快。 受到遮帘作用影响,既有隧道上方地层竖向位移出现了先增加后减小的趋势,即隧道上方的地层最大沉降处位置距既有隧道顶部仍有一定距离。 随着间距 H 增大,遮帘效应影响范围减小。
摘自《地下空间与工程学报 》