0 引言
随着设计理论的完善、施工方法的改进和新材料的使用,斜拉桥的发展进入一个崭新的时代。斜拉桥设计自由度很大,可以通过调整索力来改变结构的受力状态,一旦斜拉桥结构布置确定,总能找出一组索力,使结构在确定性荷载作用下,某种反映受力性能的指标达到最优。这组索力对应的成桥状态就是对应指标下的合理成桥状态,求解这组最优索力,并设法通过施工加以实施,也就实现了斜拉桥的成桥状态优化。因此斜拉桥承载状态的优化也就转化为斜拉桥索力优化问题。
斜拉桥是高次柔性超静定结构,而且在施工过程中结构体系不断转换,如何确定在施工中斜拉索的初张力和体系完成后的二次张拉索力,以达到设计理想状态并非容易的事情。
斜拉桥的调索方法较多,目前比较常用的主要有刚性支承连续梁法、零位移法、倒拆和正装法、无应力状态控制法、内力平衡法等[1]。
ANSYS 软件是融结构、热、流体、电磁场、声场和耦合场分析于一体的大型通用有限元分析软件。作为通用有限元分析软件,ANSYS 软件为桥梁结构有限元分析提供了新的途径,可以根据各种理论编制ANSYS 程序以更好地满足桥梁结构分析要求。根据以往的ANSYS 使用经验结合五种调索理论总结出一套切实可行的ANSYS 调索手段,可以综合比较出各种调索理论的优缺点[3],便于设计者比选出最优设计索力。
1 调索理论及模型计算
本文利用索的实际索力作为控制变量,找出索力的变化规律,建立计算模型,给出各种调索理论的计算数值,进而可以进行综合比选,选出成桥的最优索力。
什么是最优索力?关键是塔直梁平:
(1)塔要直———主塔尽量承受轴向压力。
(2)梁要平———主梁尽量弯矩比较均匀。
(3)索力均匀———短索索力小,长索索力大。
(4)支座反力———支座不能出现负反力。
为了着重探讨调索理论及其方法,对其中许多其他因素进行了忽略。例如,不考虑主塔的变形与受力影响,不考虑主梁的收缩徐变等因素,并且采用塔、梁、墩固结的刚构体系。即以图1 的三索系统为例,来说明斜拉桥的调索理论及ANSYS 计算方法。
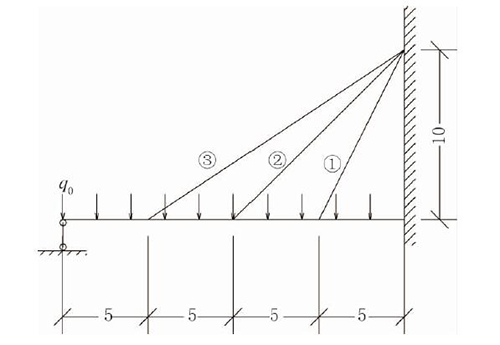
图1 三索系统示意图(单位:m)
假设已知钢索的抗拉刚度为EA1=105 kN,主梁的抗拉刚度为EA2=2.1×106 kN ,抗弯刚度EI 为2.1×105 kN•m2,均布载荷q0=100 kN/m,并假设三根索受力之前,设计载荷q0 已经作用在梁上,即全部主梁架设成功后再开始张拉3 根索。
下面以图2 的模型为例,分别介绍各种调索理论及在ANSYS 中对模型调索的实现方法。
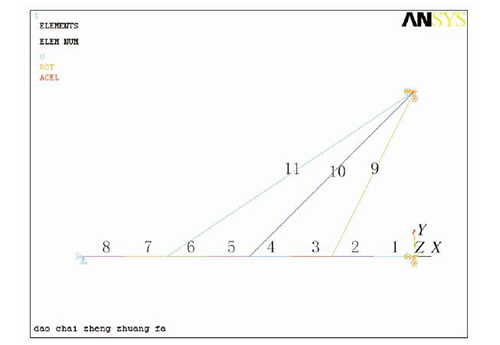
图2 ANSYS 有限元模型
1.1 刚性支承连续梁法
刚性支承连续梁法是指在成桥状态下,斜拉桥主梁的弯曲内力和刚性支承连续梁的内力状态一致,因此可以非常容易地根据连续梁的支承反力确定斜拉索的初张力。
需要说明的是,当主梁具有纵坡时,刚性支承连续梁法的计算结果不能使主梁弯矩真正达到刚性支承连续梁的相应值,而且由于在主塔附近的一段距离内一般不布置斜拉索,按刚性支承连续梁法确定的索力使得靠近主塔的第一对索力很大,而第二对索力很小,甚至出现负值。
ANSYS 实现刚性支承连续梁调索的方法如下:
(1)在索梁交点位置建立刚性杆,下端固结,索力置零,按该法求出各个刚性杆的轴力(见图3)。
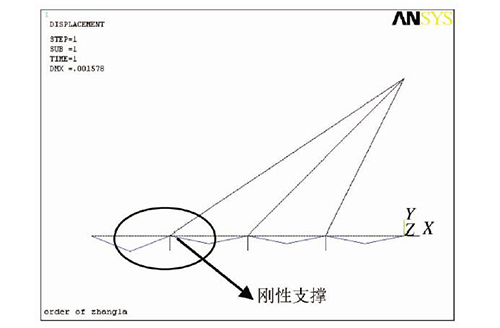
图 3 刚性支承连续梁法
(2)根据刚性杆的轴力反算出拉索的轴力,并将刚性杆的刚度置零或直接去掉刚性杆(见图4)。

图4 去除刚性支承后迭代索力
(3)将拉索的轴力乘上系数反复迭代直到结构受力和变形趋于合理。
1.2 零位移法
零位移法的出发点是通过索力调整,使成桥状态下的主梁和斜拉索交点的位移为零。
需要说明的是,以上这两种方法(刚性支承连续梁法和零位移法) 用于确定主跨和边跨对称的单塔斜拉桥是最有效的,当主跨和边跨不对称时几乎失去了作用,因为这两种方法必然导致较大的塔根弯矩,失去了索力优化的意义。
ANSYS 实现零位移调索的方法如下:
(1)将索力作为设计变量,各个拉索与主梁的交点的竖向位移为目标函数。
(2)ANSYS 将反复迭代设计索力直到竖向位移满足要求(见图5)。

图5 零位移法
1.3 倒拆和正装法
倒拆和正装法是斜拉桥安装计算广泛采用的一种方法,通过倒拆、正装交替计算,确定各施工阶段的安装参数,使结构逐步达到预定的线形和内力状态。由于斜拉桥几何非线性和混凝土收缩徐变的影响,倒拆和正装计算中,两者会不闭合,即按照倒拆的数据正装,结构偏离预定成桥状态的线形和内力状态,这时需要综合考虑混凝土收缩徐变的影响。
ANSYS 实现倒拆和正装调索的方法如下:
(1)刚性支承连续梁全桥调平,求出对应的索力。
(2)用单元生死手段实现倒拆和正装。
(3)此方法的关键是,一定要保证正装残余索力和倒拆残余索力相等。
1.4 无应力状态控制法
无应力状态控制法分析的基本思路是:不计斜拉索的非线性和混凝土收缩徐变的影响,采用完全线性理论对斜拉桥解体,只要保证单元长度和曲率不变,则无论按照何种程序恢复还原后的结构内力线形将与原结构一致。应用这一原理,建立斜拉桥施工阶段和成桥状态的联系。
考虑结构在荷载作用下变形后斜拉索两端节点的几何长度扣除斜拉索单元轴力产生的伸长量后即是斜拉索的无应力索长[4]。
则该例子中的无应力索长即为不受力状态下两个锚固点间的距离:
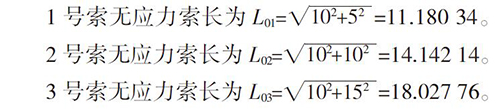
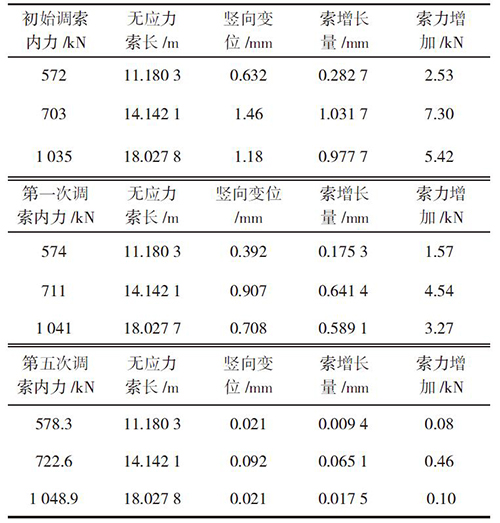
现将拉索均按照理想成桥状况的索力进行张拉(此索力为其余调索方法求出的索力平均值),张拉后各个拉索均有了初始内力。算出各个拉索的伸长长度,并算出各个拉索的竖向变位值,见表1。
表1 无应力状态法调索结果
根据竖向位移h 算出实际索长L(见图6):
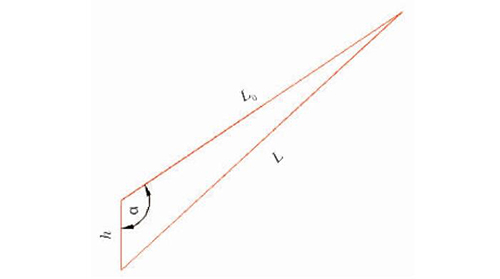
图6 索长计算图
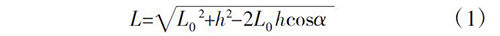
式中:L0为无应力索长;h 为锚固点竖向变形;L 为拉索实际长度;α 为拉索与竖向位移的夹角。
通过计算可求得各个锚固点的竖向变形(见图7),可明显看到各个锚固点的变形均小于1.5 mm,根据变形差求出需要增加的索力。
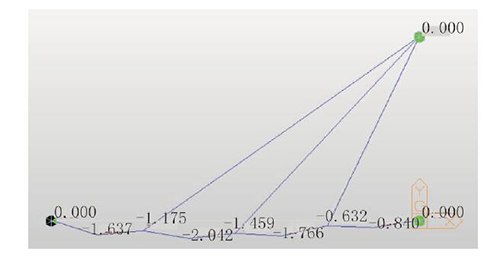
图7 初始索力作用下各个节点的变形(单位:mm)
ANSYS 实现无应力状态控制调索的方法如下:反复迭代索力值直到拉索的两个锚固点之间的距离为无应力索长(见图7)。
在初始索力作用下,各个拉索节点均有一定的变形,此时各个拉索锚固点变形均小于1.5 mm。
根据拉索伸长量对拉索索力进行微调,调整后各个拉索的索力计算结果见表1。经迭代计算拉索伸长量可控制在0.1 mm 以下,索力增加值可精确到0.1 kN,工程精度一般控制在2%以下,故调索索力满足设计要求。囿于篇幅本文只摘抄初始张拉、第一次和第五次调索结果,如图8、图9 所示。
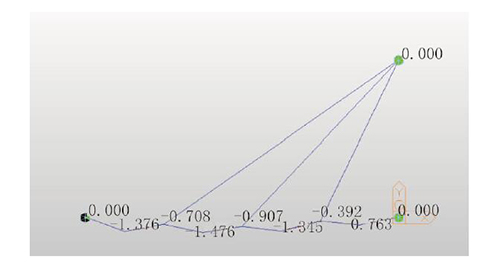
图8 第一次调索力作用下各个节点的变形(单位:mm)
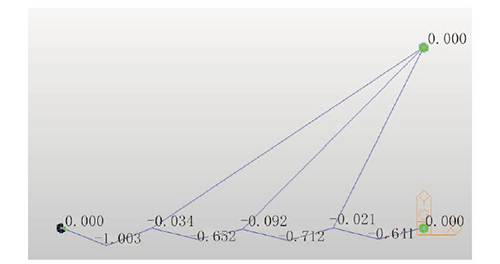
图9 第五次调索力作用下各个节点的变形(单位:mm)
第一次调索时,各个拉索锚固点变形均小于1 mm。
第五次调索时,各个拉索锚固点变形均小于0.1 mm。
1.5 内力平衡法
内力平衡法的基本原理是设计适当或合理的斜拉索初始张力,以使结构各控制截面在恒载和活载共同作用下,上翼缘的最大应力和材料允许应力之比等于下翼缘的最大应力和材料允许应力之比。
ANSYS 实现内力平衡调索的方法如下:
将单元抗弯刚度取为实际值的1/1 000,施加结构自重等外载荷,做一次落架线性计算,所得索力就是弯曲能量最小时候的最优索力,局部调整单元抗弯刚度、支承刚度和拉索抗压刚度,进一步优化结构内力,可将其作为斜拉桥成桥合理状态[2],弯矩如图10 所示。
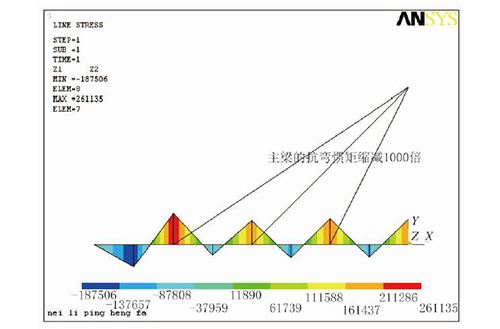
图 10 内力平衡法弯矩图(单位:N•m)
2 结语
以上文各种调索理论对举例模型进行调索计算,各种方法下各个主梁单元的内力以及拉索索力汇总见表2、表3。
表2 不同调索方法计算的主梁内力汇总kN•m
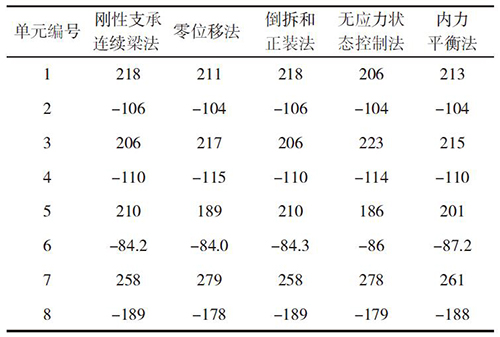
表3 不同调索方法计算的索力汇总kN
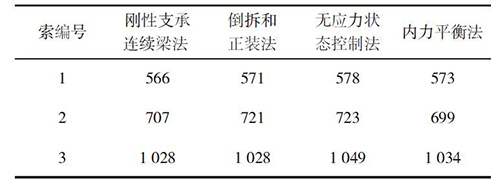
基于现有调索方法,ANSYS 可以用不同的手段实现全桥调索。对于常规杆系结构来说,上述五种方法均能实现全桥调平,但是结合具体桥梁资料,可以选择一种最优的调索结果使得全桥的内力和变形相对最优。
摘自:城市道桥与防洪