0 引言
隧道深浅埋的划分一直是学术界和工程界较为关注的问题,分界深度的不同对于计算隧道衬砌所受围岩压力的大小有着很大的影响。铁路隧道设计规范[1]和公路隧道设计规范[2]在计算围岩压力时,都将隧道埋深分为深埋和浅埋。隧道深埋与浅埋的界定以隧道拱部上覆围岩能否形成压力拱为原则确定。
由于规范[2]是建立在我国417 座单线铁路隧道的1046 个塌方样本的基础上的,现行的规范[2]在计算双线或多线等大跨度隧道的深浅埋分界深度时,虽然引进了跨度修正系数,但该系数具有较强的经验性,依据不足。近年来王明年等[3]推导出了大断面黄土隧道的深浅埋计算公式; 张佩等[4]分析了土压力拱效应提出了深埋隧道和浅埋隧道的划分方法; 朱正国[5]、宋玉香等[6]建议将岩柱理论的极大值点作为隧道的界限埋深; 高峰等[7]还考虑了动力作用对隧道埋深界限的影响;郑颖人等[8]通过研究隧洞破坏机理提出了隧道深浅埋划分标准。目前各种隧道深浅埋分界深度计算方法在小跨度的隧道和黄土隧道较为完善,随着隧道跨度的增大,隧道深浅埋界限深度计算方法不足之处日益突出,故找出一种新的界限深度计算方法显得较为迫切。
1 常用的深浅埋深度计算方法
1.1 太沙基理论深浅埋分界
太沙基将岩体视为散粒体,推导出了分界深度计算公式。
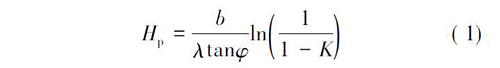
式中: λ 为侧压力系数; φ 为岩体内摩擦角; b 为松动半宽; K =σv /σvmax。
1.2 普氏理论的深浅埋分界
普氏也将围岩视为散粒体,但考虑了结构面上存在的凝聚力( 黏结力) 得出分界深度为:
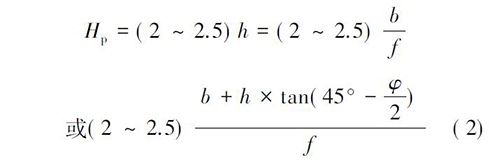
式中: φ 为围岩的内摩擦角; b 为平衡拱半跨度; f为围岩的坚固性系数; H 为隧道净高。
1.3 比尔鲍曼法深浅埋分界
比尔鲍曼法在划分隧道深浅埋分界时,考虑了真实黏聚力和内摩擦角等参数,即:
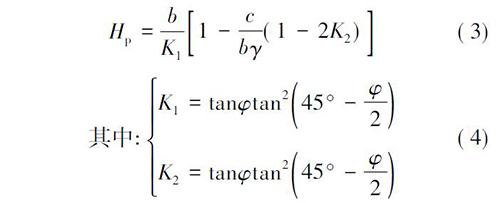
式中: γ 围岩重度; b 为隧道半跨宽度; c 为围岩的黏聚力。
1.4 等效荷载高度深浅埋分界方法
目前我国设计规范[2]均采用等效荷载高度的深浅埋分界方法,其判别式如下:
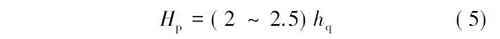
式中: Hp为隧道深浅埋分界深度,m; hq为荷载等效高度,m。
在按照矿山法施工的条件下,采用钻爆法施工的隧道: Ⅰ~Ⅲ级围岩取Hp = 2hq; IV~ VI 级围岩取Hp = 2.5hq。
我国结合417 个单线铁路隧道施工塌方资料,统计整理拟合得出平均塌方高度Hq,即荷载等效高度Ho,可按下式计算:
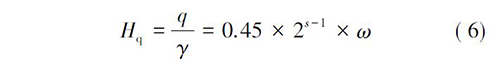
即隧道深浅埋分界深度为:
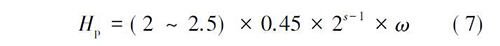
式中: s 为围岩级别; ω 为宽度影响系数,ω = 1+i×( B-5) ; i 为B 每增减1 m 时围岩压力的增减率,以B = 5 m 的围岩垂直均布压力为准,当B < 5 m时,取i = 0.2,当B>5 m 时,取i = 0.1。
该计算公式必须同时满足下列条件:
①采用钻爆法开挖的隧道;
②隧道开挖断面高宽比H/B<1.7;
③不产生膨胀力的围岩及偏压不显著的隧道;
④隧道开挖跨度小于15 m。
2 常用分界深度计算方法比较分析
从表1 可知,比尔鲍曼公式和太沙基理论综合考虑了隧道宽度B、围岩重度γ、内摩擦角φ 和黏聚力c 等4 种因素的影响,较为全面地反映了围岩物理力学指标和工程因素对围岩压力计算的影响;然而这两种方法以围岩压力计算公式得出最大值时的埋深作为深浅埋分界限,使得埋深划分的较深。
表1 围岩压力计算方法特征比较

相较而言,虽然规范[2]中仅考虑了隧道宽度B和围岩级别s 的影响,没有直接考虑内摩擦角和黏聚力的影响,但这两种因素均已在围岩分级中体现出来。而且由于规范[1]是建立在我国417 座铁路隧道的1 046 个塌方样本的基础上,这些隧道的塌方平均高度数据本身就反映了地质条件和工程因素对隧道围岩压力的影响,因此规范[1]计算方法考虑较为全面。然而这种计算方法也有着局限性,主要体现在以下3 个方面:
( 1) 以往新建或改建的隧道大部分为单线隧道,统计隧道的跨度较小,跨度大部分在5~7 m,运用于跨度较大的隧道,显然不够恰当。
( 2) 为了使公式也能在双线或多线隧道上应用,引入了宽度影响系数ω = 1+i×( B-5) ,式中比率i 是凭经验选取的( 其取值B>5 m 时,i = 0.1; B<5 m,i = 0.2) ,科学依据不足。
( 3) 统计隧道的断面形式过于单一。样本多取自马蹄形断面,因此对于当前的扁平断面的实用性值得商榷。没有充分考虑围岩的自承载能力,如图1 所示,当隧道开挖宽度大于12 m 时,深浅埋分界线小于普氏理论计算结果,在深埋情况下,无法保证塌落拱的形成。
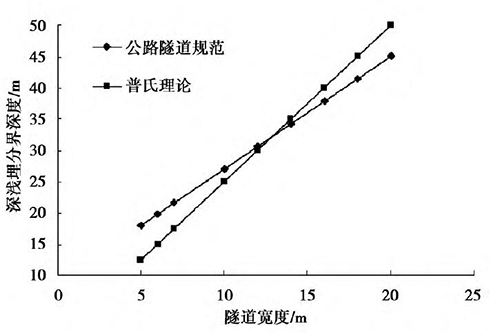
图1 隧道宽度与深浅埋分界深度关系
3 分界深度计算公式的推导
圆形隧道围岩塑性区范围可以根据围岩应力的分布特征确定,求解的基本原理是塑性区与弹性区分界处既满足塑性条件又满足弹性条件。假设塑性区中c、φ 值为常数,支护阻力为0,侧压力系数为1,求得此时塑性区半径R0。
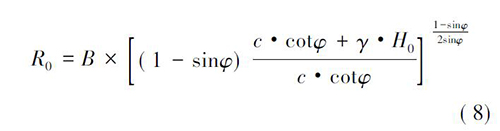
式中: B 为隧道开挖宽度,m; H0为隧道埋深,m;c 为岩体黏聚力,MPa; φ 为围岩内摩擦角,( °) 。
由式( 8) 可知,在开挖宽度B 一定的情况下,围岩塑性区半径取决于埋深H0的共同作用,塑性区半径随埋深H0增大而增大,随岩体强度c、φ 增大而减小,即埋深越大越容易形成塑性区。
对我国417 个单线铁路隧道施工塌方高度统计分析得到平均塌方高度,以及对应的隧道开挖宽度如表2 所示。
表2 铁路隧道塌方高度统计
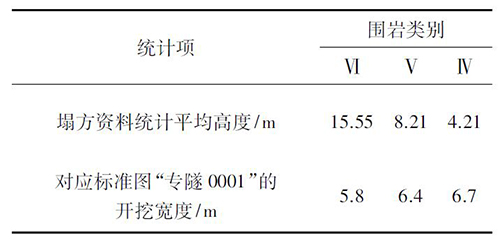
由统计结果可知,隧道塌方高度与隧道开挖宽度和围岩级别有着密切的关系,同时围岩级别和围岩力学参数有着密切关系。根据塌方高度统计资料拟合分析得到了现有铁路隧道规范中的深浅埋分界公式,该公式既有难得的实际塌方统计数据又有理论分析,从应用结果来看,对以往开挖宽度较小的铁路隧道是比较合适的。
对于研究目前大跨度隧道深浅埋分界方法时,应充分结合以往统计数据和研究成果。按现行铁路规范计算公式,计算隧道宽度分别为5、6、7 m 时的深浅埋分界深度是较为准确的。另外,由于Ⅳ级及Ⅳ级以上围岩在埋深较浅时未出现塑性区,其监测到的松动压力主要为爆破引起的围岩过度松弛,产生塑性区与松动区,造成围岩压力过大。因此,为便于讨论大跨度深浅埋分界深度与围岩塑性区大小的关系,本文主要选取围岩强度较低的Ⅴ级围岩进行分析。
喻波等[9]的研究结果表明,马蹄形隧道的压力拱为环状体,根据这一发现,圆形隧道与马蹄形隧道形成的压力拱的差异可以忽略不计。因此,将马蹄形的隧道用圆形隧道来进行简化,简化的原则是隧道宽度保持不变。Ⅴ级围岩力学参数按规范建议平均值取值,围岩重度γ = 18.5 kN/m3、内摩擦角φ= 23.5°、黏聚力c = 0.125 MPa,隧道宽度分别为5 m、6 m、7 m。将参数分别代入式( 8) ,求得当隧道埋深处于深浅埋分界时围岩塑性区半径大小,计算结果如表3。
表3 不同开挖宽度深浅埋分界与塑性区半径m
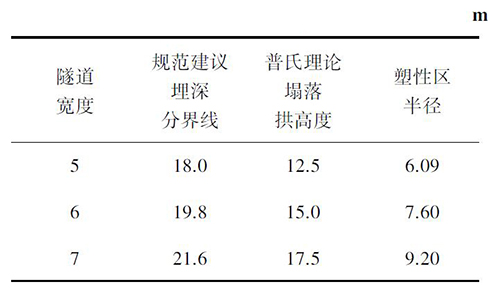
塑性区半径和隧道深浅埋分界深度随着开挖半径的增大而逐渐增大。同时,规范建议值大于普氏理论计算值,可以形成平衡拱,也说明在开挖宽度不大的情况下,采用规范建议值是合适的。深浅埋分界深度与塑性区半径关系如图2 所示。

图2 深浅埋分界深度与塑性区半径关系
隧道深浅埋分界与塑性区半径间关系为:
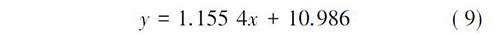
设隧道埋深为H,塑性区半径为R0,隧道半径为B,当埋深满足式( 9) 时,此时H = Hp,即为隧道深浅埋分界深度,将式( 8) 代入式( 9) ,求解Hp:
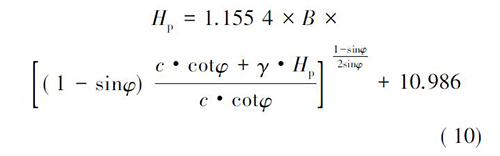
式( 10) 即为Ⅴ级围岩不同开挖宽度时的深浅埋分界公式。公式表明,隧道深浅埋划分的临界深度与隧道开挖宽度B、围岩的黏聚力C、围岩的内摩擦角φ 和围岩重度γ 密切相关,当围岩力学性质一定时,分界深度与隧道开挖宽度呈线性关系。将Ⅴ级围岩平均力学参数代入式( 10) ,可简化为:

该方程为一元多次方程,需通过MATLAB 软件求解。
分别按《公路隧道设计规范》、普氏理论和本文公式3 种方法计算不同开挖宽度时的深浅埋分界深度,将3 种方法的计算结果进行对比,如表4和图3 所示。
表4 不同开挖宽度的隧道深浅埋分界深度m
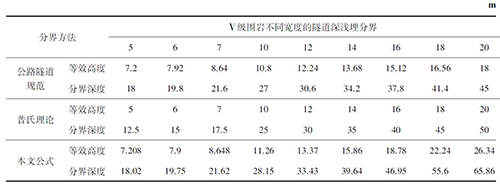
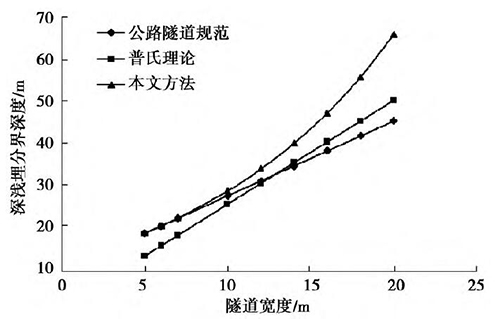
图3 不同计算方法的隧道深浅埋分界深度对比
在隧道宽度较小时,本文公式的深浅埋分界深度与规范建议值较吻合,说明其计算结果较符合隧道塌方统计平均高度。随着开挖跨度的增大,本文计算结果与公路隧道设计规范的计算结果相差增大。本文公式计算结果始终大于普氏理论计算值,说明按照其计算方法,可以保证在深浅埋分界深度时塌落拱的形成,也说明本文计算方法科学合理。
4 等效荷载高度与分界深度实测统计分析
本文收集了国内103 座Ⅴ级围岩不同跨度隧道塌方资料,包括塌方段的埋深、开挖跨度、塌方高度等,可为隧道的等效荷载高度和深浅埋分界深度提供有价值的数据支撑。
由表5 可知,塌方次数与开挖跨度成正比关系,开挖跨度越大,塌方次数越多; 当开挖跨度大于13 m 时,塌方次数反而减小。其主要原因为: 一是目前我国开挖跨度过大的隧道尚比较少见,统计样本较少,参考性较低; 二是当开挖跨度过大时一般采用分步开挖等方式,实质上是降低了一次开挖的跨度; 三是当开挖跨度过大时,一般采用的支护强度也很大,在一定程度上也降低了产生塌方的概率。
表5 不同跨度塌方类型统计
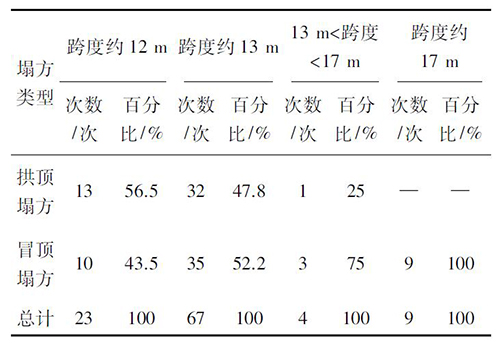
从塌方类型上来看,随着开挖跨度的增大,发生拱顶塌方的概率越来越小,而发生冒顶塌方的概率则越来越大。跨度从12 m→13 m→17 m,冒顶塌方的概率从43.5%→52.2%→75%→100%。这也说明,在埋深一定的情况下,开挖跨度越大,围岩稳定性越差,越难以形成稳定的塌落拱,越容易发生冒顶塌方。隧道埋深不同,围岩破坏模式也不同。当隧道处于深埋状态时,塌方形态多为拱形; 浅埋状态时,则多为冒顶塌方。
通过统计分析,得到了隧道埋深与塌方发生事件之间的关系,如图4 和图5 所示。从图中可以看出,在开挖跨度为12 m 时,所有发生冒顶塌方的隧道埋深均小于37 m,当埋深大于37 m时,在统计的资料范围内未见冒顶塌方,均为局部塌方,说明开挖跨度为12 m 时,当埋深大于37 m 时,一般均已形成了稳定的塌落拱,塌方不再继续向上发展,只有塌落拱范围内的岩体发生了垮塌。在开挖跨度为17 m 时,统计范围的塌方事件均为冒顶塌方,最大冒顶深度达64 m。由于开挖跨度为12 m、17 m 的隧道统计资料有限,尚无法根据已有资料明确形成塌落拱所需的隧道埋深; 但统计表明,冒顶塌方多发生在浅埋状态,随着埋深的增大,到达深埋状态时,形成稳定的塌落拱后,塌方形态则变为拱形塌方。这一结论对通过塌方资料统计来确定隧道深浅埋分界具有重要意义。
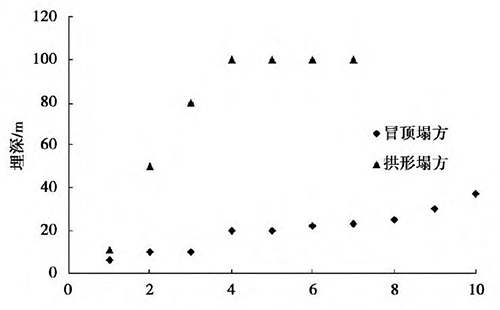
图4 隧道塌方与埋深的关系( 跨度为12 m)
以上分析表明,塌方形态和塌方高度与隧道深浅埋性质和等效荷载高度有密切的关系。
5 统计数据和模型试验与计算结果对比分析
在本文隧道塌方的统计资料中,最为常见的、样本最多的为开挖跨度约为13 m 的隧道,故以此为基础,探讨等效荷载高度及深浅埋分界深度与塌方数据关系,并与本文公式相对比验证。
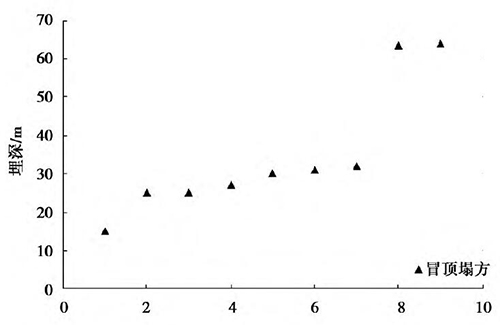
图5 隧道塌方与埋深的关系( 跨度为17m)
对塌方次数随埋深的变化规律分析可以得知,隧道开挖跨度为13 m 时,拱形塌方最高埋深为380 m; 冒顶塌方最高埋深为180 m,其中85.96%的冒顶塌方发生在埋深40 m 及以下,如图6 所示。同时由图7 可知,随着埋深的增大,冒顶塌方发生的概率越来越小,拱形塌方发生的概率则越来越大。资料显示,冒顶塌方的平均埋深为32. 44 m,且当埋深≤32 m 时,全部为冒顶塌方,说明此时埋深并不足以形成稳定的塌落拱,隧道仍处于浅埋状态。而按《公路隧道设计规范》计算,当埋深为32. 4 m 时,隧道已处于深埋状态,可以形成塌落拱,此时塌方形态多为拱形塌方,这与现场实际不相符,因此也说明隧规计算结果对大跨隧道深浅埋划分具有一定局限性。
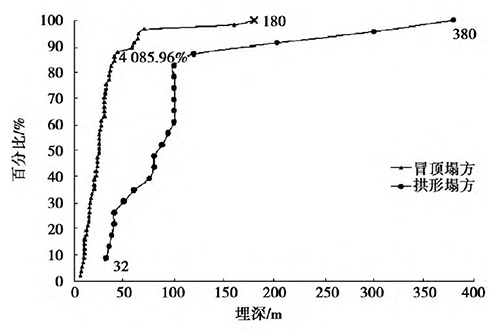
图6 塌方概率随埋深变化规律
图6 表明,当埋深大于32 m 时,拱形塌方开始出现,并随着埋深的增大,占塌方的比例也越来越大。当埋深大于40 m 时,拱形塌方在所有塌方类型中已占较大比例,说明在此埋深下,围岩塌落拱已基本形成,属于深埋隧道。当埋深为32 ~ 40 m时,拱形塌方与冒顶塌方所占比例相当,各为50%,因此可以确定深浅埋的临界埋深应在32 ~40 m之间,开挖跨度为13 m 的隧道深浅埋分界深度为36 m。
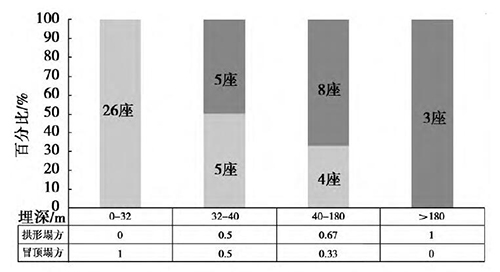
图7 不同埋深段不同塌方类型占总塌方的比例
将本文方法与普氏理论和公路隧道设计规范计算方法得到的计算结果和实际统计塌方高度的平均值相比较( 如表6) 可知,本文方法与实际结果最为吻合,深浅埋分界深度与实际结果偏离度仅为1.11%,普氏理论次之,公路隧道设计规范理论与结果相差最大。
此外,从偏离度可知,3 种计算理论中,只有本文方法计算结果比实际结果偏大,说明按此理论进行支护设计时,隧道更偏于安全。
表6 塌方统计高度与理论计算对比
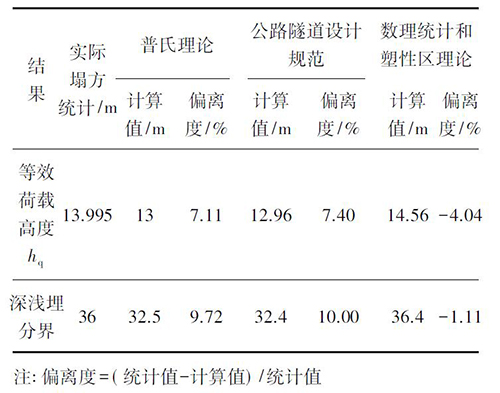
此外,中国建筑科学研究院汪成兵[10]曾采用模型试验方法对开挖净宽为11 m 的隧道塌落拱高度进行了模拟研究( 如图8) 。结果表明,当隧道埋深分别为10、20、30 m 时,围岩始终无法形成稳定的塌落拱,以致塌落拱持续向上发展,最终到达地表,形成冒顶塌方如图9 所示。因此,对于开挖跨度为11 m 的隧道,埋深达30 m 时,仍无法形成稳定的塌落拱,仍处于浅埋状态。而按照公路隧道设计规范及普氏理论计算,对于开挖跨度为11 m 的隧道,埋深大于28.8 m 时,隧道已处于深埋状态,塌方形态应为拱形塌方,这与模型试验结果不相符合。但按推导计算方法计算,深浅埋分界深度为30.69 m,所以埋深为30 m 时为浅埋隧道,塌方主要为冒顶塌方,与试验结果相一致。
因此,通过对塌方数据的统计和模型试验分析,综合比较3 种理论,显然本文方法更符合现场实际,也更能指导隧道支护设计。
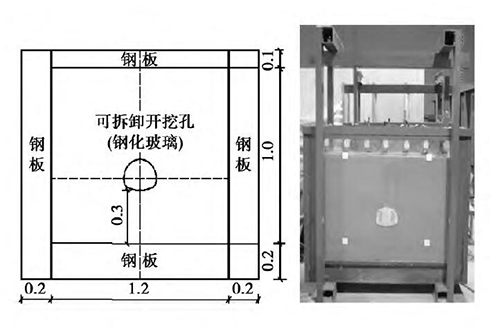
图8 试验模型( 汪成兵)

图9 不同埋深最终破坏形态( 10、20、30 m,汪成兵)
6 结论
(1) 通过对20 世纪70 年代成昆、贵昆、川黔等铁路417 个单线铁路隧道施工塌方统计资料的分析,并结合提出的深浅埋划分准则,推导出了隧道深浅埋划分界限的理论公式。该公式充分考虑了开挖后围岩应力状态的调整变化,又结合了大量的塌方统计资料,具有较高的可靠性和工程应用价值。
(2) 通过对国内不同跨度的103 座Ⅴ级围岩隧道进行塌方统计,求得实际等效荷载高度和深浅埋分界深度; 将其结果与不同深浅埋分界理论计算结果相比较,并结合隧道塌方模型试验,证明基于统计和塑性区理论深浅埋划分计算方法在计算大跨度隧道深浅埋界限深度时是合理可信的,能够更好地为工程设计实践提供科学的依据。
摘自:地下空间与工程学报