0 引言
盾构已广泛应用于地下交通、运输管道等隧道工程建设。在掘进过程中盾构刀盘与土体之间的相互作用十分复杂,因此,研究分析盾构刀盘切削土体向前掘进的过程十分重要。分析掘进过程中刀盘的受力情况及刀盘与土体的适应性对优化刀盘设计具有一定的指导意义。
由于盾构刀盘的作业空间在地表以下,因此其具体的运动情况以及刀盘与土体之间的相互作用无法直接观测。目前,关于盾构掘进的研究大多侧重于单个切削具(切刀、滚刀)切削岩土体的过程,而考虑整个刀盘与土体之间相互作用的研究较少。以往主要通过简化理论、模型试验和数值计算3种方法对盾构刀盘掘进过程进行研究。在理论研究方面:宋克志等[1]给出了盾构刀盘扭矩的估算公式;管会生等[2]__________分析了刀盘扭矩的构成因素,建立了扭矩估算的理论模型;施虎等[3]推导了掘进过程中刀盘迎面阻力计算公式。在模型试验方面:吕强等[4]针对面板式和辐条式刀盘进行了模型试验,结合试验得到的扭矩结果导出了扭矩计算的经验公式;苏健行等[5]建立了土压平衡盾构掘进过程中总推力的数学计算模型,然后以模型试验所得结果验证了其模型的准确性。在数值计算方面:目前大多数研究考虑的是静态情况[6-9],即采用ANSYS、SolidWorks等软件建立刀盘的简化模型,然后施加预定荷载,得出刀盘各部分的应力应变情况,不能反映整个掘进过程中土体的破坏过程及刀盘受力随时间的变化情况。由于刀盘尺寸与土体颗粒尺寸的差异巨大,土体变形属于大变形过程,所以在进行动态数值模拟研究时会遇到很多困难,关于这方面的研究基本还停留在初级阶段。SHEN等[10]采用任意拉格朗日-欧拉法(ALE)方法,从流固耦合角度处理了刀盘与土体之间的相互作用,分析了刀盘掘进的过程;苏翠侠等[11-12]采用ABAQUS软件模拟了刀盘掘进过程,并分析了影响刀盘载荷的因素;陈馈等[13]采用ANSYS软件对刀盘的应力分布进行分析,得到了刀盘刮刀承受轴向分力的分布规律。
为了研究土压平衡盾构刀盘掘进过程中的土体变形及刀盘受力问题,采用大型通用有限元分析软件ABAQUS分别建立了在砂土和黏土地层条件下刀盘掘进的动态仿真模型,基于仿真结果,讨论了掘进过程中土体的变形破坏过程及刀盘所受载荷的变化规律。
1 刀盘模型及土体材料参数
盾构刀盘与土体的相互作用是高度非线性的,影响这一过程的因素很多。在建立仿真模型时,进行适当简化,模型包括盾构刀盘以及刀盘正前方接触的土体。
1.1刀盘模型以图1所示的盾构刀盘为原型,进行适当简化建立刀盘仿真三维模型,如图2所示。在建立刀盘模型时,先分别建立刀架和切刀的模型,再组合成为一个整体刀盘模型。由于切刀是焊接在刀架上,且对刀盘掘进过程整体受力的影响很小,在计算模型中忽略了切刀和刀架之间的相互作用以减少计算量。刀盘直径为6140mm,厚度为450mm。在建立模型时刀盘材料采用各向同性的线弹性材料,其物理力学参数见表1。

图1 盾构刀盘实物图

图2 盾构刀盘模型图
表1 刀盘及土体材料参数

1.2土体模型
刀盘掘进过程中土体材料性质将直接影响刀盘受力和土体切削的效果。在综合考虑计算精度和效率的基础上适当选取土体模型,本文所选取的土体模型大小为6500mm×6500mm×100mm。
ABAQUS软件对经典的Drucker-Prager模型进行了扩展,可以用来模拟含有摩擦角和黏聚力的材料,而土体材料是其中较为典型的一种,所以本文在进行仿真计算时,将与刀盘相互作用的土体材料的本构关系通过线性Drucker-Prager模型的屈服准则来模拟[14]。
线性Drucker-Prager模型在π平面上的屈服轨迹如图3所示,其屈服准则的表达式为F=t-ptanβ-d=0;(1)
t=q/2[1+1/κ-(1-1/κ)(r3/q)]。(2)
式中:t为偏应力;p为等效压应力;β为线性屈服面在p-t应力空间上的倾角,即材料的摩擦角;d为屈服面在应力空间t轴上的截距,即材料的黏聚力;q为Mises等效应力;κ为三轴拉伸强度与三轴压缩强度之比,反映主应力对屈服的影响(其中κ=0.8时为曲线n,κ=1.0时为曲线m);r为偏应力第三不变量。
在模拟掘进过程中,土体单元的损伤破坏及切屑分离是一个难点,土体材料受到载荷作用时,土体从屈服到破坏是一个连续变化的过程,ABAQUS将此过程描述成屈服应力软化和弹性模量退化的过程。为了模拟土体单元的生死情况,ABAQUS引入基于损伤演化的应力-应变曲线,如图4所示。
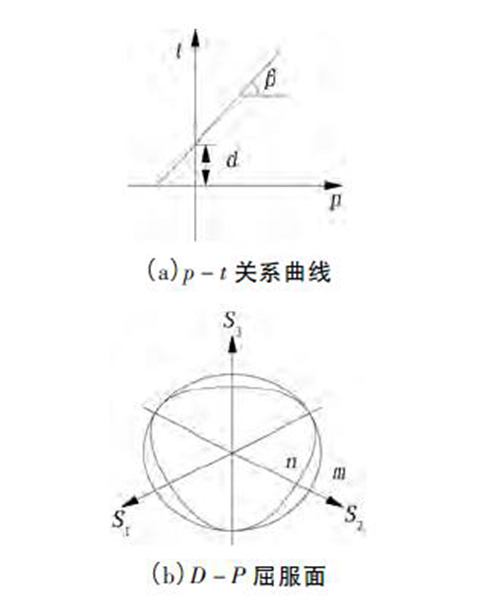
图3 扩展线性Drucker-Prager模型
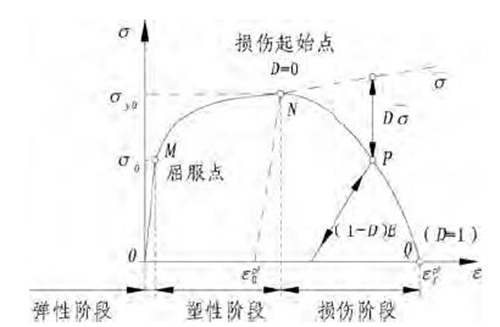
图4 土体的应力-应变曲线
图4中:D为损伤变量,σy0和εpl0分别为土体材料损伤破坏初期对应的应力和等效塑性应变,εplf为土体材料完全损伤破坏时的等效塑性应变,珚σ为忽略材料损伤的应力张量。土体单元损伤失效过程包含4个阶段:OM阶段为弹性变形阶段,MN为塑性变形阶段,NP为损伤演化阶段,PQ为应力软化阶段。N点为初始损伤破坏点,此时,D=0表示土体内部将形成微裂纹,这些微裂纹随着载荷的作用会在损伤累积的演化过程中形成宏观力学性能上的应力软化,表现为材料刚度减弱直至丧失其抗剪能力,NPQ段描述了材料的刚度退化和应力软化规律。此时,材料的应力张量表达式为
σ=(1-D)珚σ。__________(3)
当D=1时,即图中的Q点,土体单元处于完全失效破坏状态。图4中的虚线表示土体材料的无损伤硬化阶段。
有限元分析中模拟材料的剪切失效及切屑形成过程的方法主要有2种:1)基于应力应变能密度的物理分离准则;2)基于几何尺寸的几何分离准则。引入包含单元删除功能的材料单元损伤失效模型能有效地解决材料受载荷作用导致的大变形和交错。材料的单元损伤失效是基于特定本构关系的单元材料达到其强度极限后,材料刚度按照某一规律逐渐降低直至为零,此时,材料单元完全失去其承载能力并退出模型的计算。在ABAQUS中的剪切失效准则模型是基于单元积分点的等效塑性损伤模型。该模型定义了描述等效塑性应变εpl递增的状态量ωs来确定材料单元是否失效。其中
ωs=∫dεpl/εpl(θs,珔εpl);(4)
θs=(q+ksp)/τmax。(5)
式中:εpl为等效塑性应变;θs为应力比;珔εpl为应变率;q为Mises应力;ks为材料参数,取0.3;p为压应力;τmax为最大剪应力。当ωs=1时,材料单元达到剪切破坏准则,即达到初始破坏点N。
本文进行仿真时引入单元有效位移来定义土体材料的损伤变化规律,当材料损伤破坏时,其有效塑性位移
珔μpl=L•珔εpl。(6)
式中L为特征长度。由于土体本构模型是线性Drucker-Prager模型,故可定义损伤变量D与特征长度呈线性关系,当土体单元完全失效时(Q点),损伤变量的增量
ΔD=L珔εpl/珔μplf=珔μpl/珔μplf。(7)
式中珔μplf为土体单元失效时的有效位移。
在用ABAQUS进行仿真计算时,软件监测D值的变化,当D=1时土体单元完全失效,此时ABAQUS中的标记状态量会变为1,随即将该土体单元从计算模型中移除,并进行下一个土体单元的标记,依次计算便会得出计算结果。
土压平衡盾构掘进的主要工作地层为砂土和黏土地层,不适用于硬岩层。在本次研究中,选取砂土和黏土地层进行模拟。仿真采用的土体材料参数见表1[15-16],其中弹性部分的参数包括材料的杨氏模量E和泊松比μ;塑性部分的参数包括流应力比κ、摩擦角β和膨胀角ψ。
2 刀盘掘进动力学模型
将刀盘和土体模型组合起来如图5所示。初始状态时刀盘上的切刀与土体即将接触。在刀盘中心位置建立参考点RP,建立其与整个刀盘的刚体约束关系,通过控制参考点RP的运动来实现刀盘的自转和向前掘进。限制参考点RP沿X轴、Y轴的平动自由度和转动自由度,同时施加沿Z轴方向的平动速度和绕Z轴的转动速度。对于土体模型,与刀盘接触的开挖面放开全部自由度,土体背面为全约束,上下表面和前后表面为对称约束。盾构刀盘和土体之间采用非光滑的接触条件模拟,法向特性设定为硬接触,切向特性设定为采用罚函数的摩擦公式,摩擦因数为0.27。
在综合考虑实际的刀盘运动状态和数值模拟计算效率的情况下,合理设置刀盘的运动速度。设定刀盘的前进速度v=40mm/min=0.6667mm/s,刀盘的自转速度ω=1r/min=0.1047rad/s。整个仿真时间t=60s,即刀盘自转1周,向前掘进l=40mm。
刀盘和土体均采用三维八节点实体减缩积分单元(C3D8R单元)进行划分。刀盘模型共划分为117042个节点,82325个单元;土体模型共划分为637656个节点,528125个单元。
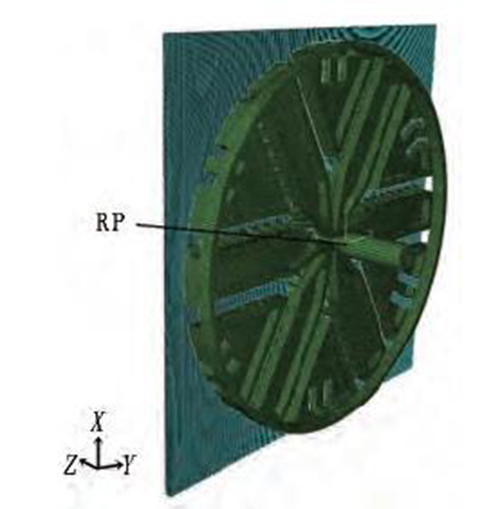
图5 刀盘掘进三维模型
3 模拟结果和分析
3.1土体切削效果
3.1.1土体塑性应变
土体在切削过程中的塑性应变反映了土体所处的状态以及刀盘和土体之间的相互作用。砂土与黏土在切削过程中的破坏方式以及等效塑性应变随时间变化的规律是大致相似的,图6为t=6s时刻黏土模型的等效塑性应变(PEEQ)云图,图中只显示土体部分,不显示刀盘部分,刀盘的转动方向为顺时针。
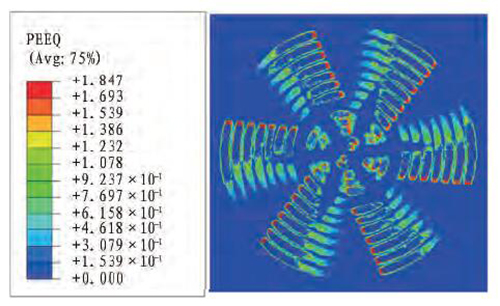
图6 土体塑性应变(黏土,t=6s)
土体与刀盘上切刀接触区域的等效塑性应变最大。沿着刀盘的转动方向,土体逐渐被切刀挤压切削,产生塑性变形,直至剪切破坏脱离土体。其他区域的土体塑性应变较小,主要在尚未与切刀接触的土体和切刀轨迹扫掠过之后已经受到剪切作用产生破坏了的土体。随着时间增长,刀盘不断回转和向前掘进,切刀不断切削土体,土体累积塑性应变而破坏。
3.1.2刀盘切削土体效率
刀盘切削土体的效率可以用土体模型质量下降速率来表征,同体积砂土和黏土的质量不同,本文选取剩余质量比(土体某时刻剩余质量×100%/原模型土体质量)的下降速度来进行衡量。图7为砂土和黏土在刀盘掘进过程中的土体剩余质量比随时间变化的关系曲线。从t=0s时刻开始,随着刀盘的掘进,土体单元不断地破坏脱离土体,土体模型质量不断减少,剩余土体质量比也相应下降。在同样的切削条件和仿真时间内,黏土模型质量比的减少量比砂土模型多。
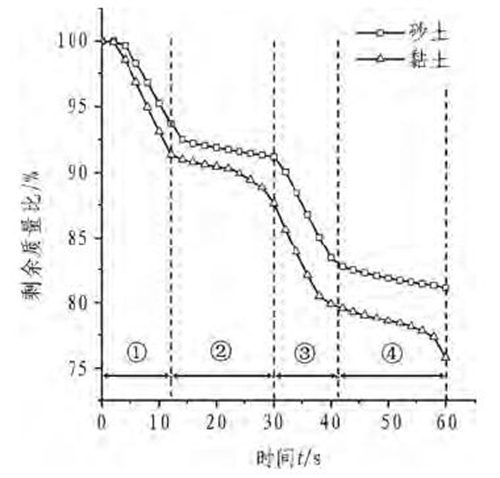
图7 土体剩余质量比与时间关系曲线
土体单元尺寸与刀盘尺寸之间相差巨大,而土体网格的划分是有限度的。土体单元的厚度为20mm,使得土体累积塑性应变达到剪切破坏时的位移较小,刀盘掘进12s时(即刀盘前进8mm)首层土体单元失效完成,而此时刀盘大部分切刀还未与第2层土体单元接触,因而在12~30s,仅有少量切刀及中心切削刃切削土体,30s时(即刀盘前进20mm)刀盘上切刀与重新形成的掌子面接触继续切削。根据上述土体切削过程可以将图7中曲线分为4个阶段,分别为①t=0~12s,②t=12~30s,③t=30~42s和④t=42~60s。各阶段刀盘切削土体速率是不同的。
将t=0s时和t=2s的土体剩余质量比的差值除以时间差得到这一时段的质量比下降速度平均值,记为v1,依次可得v3,v5,v7…,计算结果如图8所示。砂土模型和黏土模型的土体剩余质量比下降速度规律一致,呈周期性上升和下降,根据速度变化趋势可将整个掘进过程分为4个阶段,与图7中的划分一致。在其他掘进参数不变的条件下,砂土中的质量下降速率要小于黏土,表明同样条件下刀盘在砂土中的切削效率低于黏土。
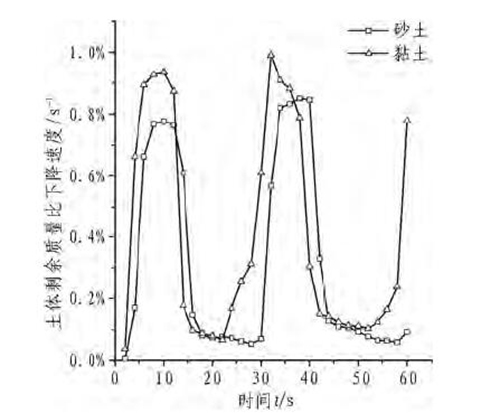
图8 土体剩余质量比下降速度与时间关系曲线
3.2刀盘受力
在仿真过程中将刀盘模型设为刚体,输出刀盘控制点RP在整个掘进过程中所受的轴向力和力矩即可反映整个刀盘的受力情况。
3.2.1刀盘轴向力
图9给出了刀盘轴向力随时间变化的关系曲线。可以看出:刀盘轴向力呈周期性变化。从t=0s开始迅速增大;到t=5s达到最大值,此时土体单元开始因塑性变形过大而陆续破坏失效;到t=12s时第1层土体单元失效完成;t=12~30s维持较小的轴向合力;t=30s时,刀盘切刀接触第2层土体单元,开始下一个切削周期。砂土模型和黏土模型中刀盘轴向力的变化规律是一致的,由于砂土与黏土材料在物理力学性质上的差异,其最大值不同。在其他掘进参数相同的条件下,刀盘在砂土模型中掘进时受到的轴向力最大值约为60kN,大于在黏土模型中掘进时轴向力最大值45kN。
3.2.2刀盘扭矩
刀盘扭矩是刀盘掘进过程中的重要参数。图10给出了刀盘扭矩随时间变化的关系曲线。与刀盘所受轴向力的变化规律一致,刀盘扭矩的变化也呈现出明显的周期性。对于黏土模型,扭矩从t=0s开始迅速增加;到t=5s时达到最大值,之后开始减小;到t=12s时趋于稳定;到t=30s时开始进入第2个切削周期。汤华等[17]采用任意拉格朗日-欧拉法(ALE)对盾构刀盘切削土体进行了仿真,得到了刀盘载荷随时间的变化情况,其规律与图10所示规律一致。砂土的物理力学性质与黏土不同,刀盘在砂土模型中掘进时的扭矩变化情况与黏土稍有差异,在t=5s达到最大值后会稳定一段时间,约到t=11.5s之后才开始迅速回落。在其他掘进参数一致的情况下,刀盘在砂土模型中掘进时受到的扭矩最大值约为200kN•m,大于在黏土模型中掘进时的扭矩最大值75kN•m。
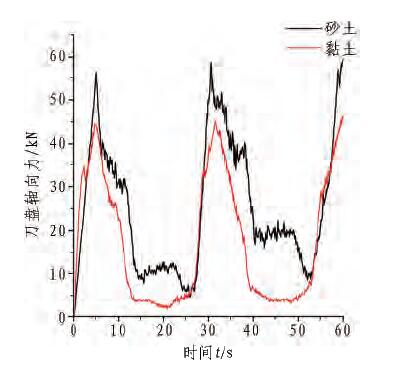
图9 刀盘轴向力与时间关系曲线
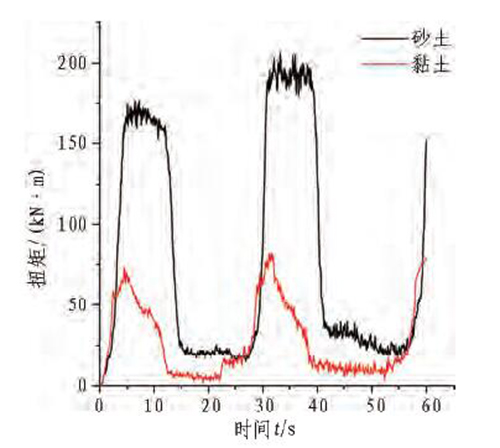
图10 刀盘扭矩与时间关系曲线
4 结论与讨论
运用大型通用非线性有限元分析软件ABAQUS建立了砂土和黏土地层条件下土压平衡盾构刀盘掘进的三维力学模型,研究了土体在切削过程中的塑性应变、切削效率及刀盘受力,结果表明:
1)土体与刀盘上切刀接触区域的等效塑性应变最大。仿真中土体单元累积塑性应变直至破坏的过程在一定程度上反映了土体受切刀作用产生一定剪切位移之后脱离土体的实际破坏过程。
2)在其他掘进参数不变的情况下,砂土模型剩余质量下降速度低于黏土,表明刀盘在砂土中的切削效率低于黏土。
3)刀盘受到的轴向力和扭矩呈现出周期性。在砂土和黏土中掘进时刀盘承受载荷的周期性规律大致相同。在其他掘进参数不变的情况下,刀盘在砂土中掘进时所受轴向力和扭矩大于黏土。
4)仿真结果能够为土压平衡盾构刀盘的设计研究提供一定的依据,以改进和优化刀盘设计。
摘自:隧道建设